题目内容
12.已知f(x)=tan(2x+$\frac{π}{4}$),则使f(x)≥$\sqrt{3}$成立的x的集合是( )| A. | [$\frac{π}{24}$+$\frac{1}{2}$kπ,$\frac{π}{8}$+$\frac{1}{2}$kπ),k∈Z | B. | (-$\frac{π}{8}$+$\frac{1}{2}$kπ,$\frac{π}{24}$+$\frac{1}{2}$kπ),k∈Z | ||
| C. | [$\frac{π}{24}$+kπ,$\frac{π}{8}$+kπ),k∈Z | D. | [$\frac{π}{24}$+kπ,$\frac{π}{8}$+kπ],k∈Z |
分析 根据正切函数的图象与性质,结合题意,即可求出不等式的解集.
解答 解:∵f(x)=tan(2x+$\frac{π}{4}$),
∴f(x)≥$\sqrt{3}$化为tan(2x+$\frac{π}{4}$)≥$\sqrt{3}$,
即$\frac{π}{3}$+kπ≤2x+$\frac{π}{4}$<$\frac{π}{2}$+kπ,k∈Z;
解得$\frac{π}{24}$+$\frac{1}{2}$kπ≤x<$\frac{π}{8}$+$\frac{1}{2}$kπ,k∈Z;
故使f(x)≥$\sqrt{3}$成立的x的集合是[$\frac{π}{24}$+$\frac{1}{2}$kπ,$\frac{π}{8}$+$\frac{1}{2}$kπ),k∈Z,
故选:A.
点评 本题考查了正切函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
20.已知x=$\frac{π}{12}$是函数f(x)=$\sqrt{3}$sin(2x+φ)+cos(2x+φ)(0<φ<π)图象的一条对称轴,将函数f(x)的图象向右平移$\frac{3π}{4}$个单位后得到函数g(x)的图象,则函数g(x)在[-$\frac{π}{4}$,$\frac{π}{6}$]上的最小值为( )
| A. | -2 | B. | -1 | C. | -$\sqrt{2}$ | D. | -$\sqrt{3}$ |
4.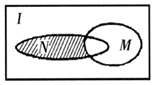 设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
 设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x<3} | B. | {x|1≤x<3} | C. | {x|1<x≤3} | D. | {x|1≤x≤3} |
