题目内容
13．函数$y=\frac{1}{3}{x^3}+b{x^2}+（b+2）x+3$在R上不是单调增函数则b范围为（ ）| A． | （-1，2） | B． | （-∞，-1]∪[2，+∞） | C． | [-1，2] | D． | （-∞，-1）∪（2，+∞） |
分析 三次函数y=$\frac{1}{3}$x3+bx2+（b+2）x+3的单调性，通过其导数进行研究，故先求出导数，利用其导数恒大于0即可解决问题．
解答 解：∵y=$\frac{1}{3}$x3+bx2+（b+2）x+3，
∴y′=x2+2bx+b+2，
∵f（x）是R上的单调增函数，
∴x2+2bx+b+2≥0恒成立，
∴△≤0，即b2-b-2≤0，
则b的取值是-1≤b≤2．
∴y=$\frac{1}{3}$x3+bx2+（b+2）x+3在R上不是单调增函数，
实数b取值范围是b＜-1或b＞2，
故选：D．
点评 本题考查函数的单调性及单调区间、利用导数解决含有参数的单调性问题，属于基础题．
练习册系列答案
中考解读考点精练系列答案
相关题目
4．
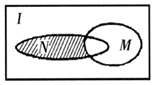设全集I是实数集R，M={x|x≥3}与N={x|（x-3）（x-1）≤0}都是I的子集（如图所示），则阴影部分所表示的集合为（ ）
设全集I是实数集R，M={x|x≥3}与N={x|（x-3）（x-1）≤0}都是I的子集（如图所示），则阴影部分所表示的集合为（ ）| A． | {x|1＜x＜3} | B． | {x|1≤x＜3} | C． | {x|1＜x≤3} | D． | {x|1≤x≤3} |
5．已知△ABC，$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{AB}$，$\overrightarrow{BD}$=$\frac{1}{3}$$\overrightarrow{BC}$，AD与CE的交点为G，$\overrightarrow{BA}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，若$\overrightarrow{BG}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$，则λ+μ=（ ）
| A． | $\frac{2}{7}$ | B． | $\frac{3}{7}$ | C． | $\frac{4}{7}$ | D． | $\frac{5}{7}$ |
