题目内容
7.已知集合$M=\left\{{({x,y})\left|{\frac{x^2}{9}+\frac{y^2}{4}=1}\right.}\right\}$,N={(x,y)|y=kx+b},若?k∈R,使得M∩N=∅成立,则实数b的取值范围是( )| A. | [-3,3] | B. | (-∞,-3)∪(3,+∞) | C. | [-2,2] | D. | (-∞,-2)∪(2,+∞) |
分析 集合M椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1上的点组成的集合,集合N={(x,y)|y=kx+b}表示过(0,b)点斜率存在的直线上的点组成的集合,则满足条件的实数b应满足(0,b)点在椭圆外,结合椭圆的性质可得答案.
解答 解:集合$M=\left\{{({x,y})\left|{\frac{x^2}{9}+\frac{y^2}{4}=1}\right.}\right\}$,表示椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1上的点组成的集合,
集合N={(x,y)|y=kx+b}表示过(0,b)点斜率存在的直线上的点组成的集合,
若?k∈R,使得M∩N=∅成立,
则(0,b)点在椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1外,即$\frac{{b}^{2}}{4}$>1,
解得b<-2或b>2,
故b∈(-∞,-2)∪(2,+∞)
故选:D.
点评 本题考查的知识点是交集及其运算,椭圆的性质,其中将已知转化为(0,b)点在椭圆外,是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.若向量$\overrightarrow p,\overrightarrow q$满足$|\overrightarrow p|=8,|\overrightarrow q|=6,\overrightarrow p•\overrightarrow q=24$,则$\overrightarrow p$和$\overrightarrow q$的夹角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
12.函数f(x)=ex-2x+1在[0,1)上的最小值是( )
| A. | 2 | B. | e-1 | C. | 3-2ln2 | D. | 2-2ln2 |
16.下列函数中,在(0,+∞)为增函数的是( )
| A. | y=x2-3x+1 | B. | y=-2x+9 | C. | $y={(\frac{1}{2})^x}$ | D. | y=log2x |
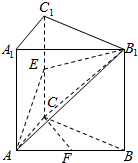 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.