题目内容
4.设正项等比数列{an}的前n项和为Sn,且满足S3=3a3+2a2,a4=8.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列bn=log2an,求{|bn|}的前n项和Tn.
分析 (Ⅰ)设正项等比数列{an}的公比为q,则q>0,根据已知条件和等比数列的通项公式求得q的值,则an=a4qn-4;
(Ⅱ)由bn=|log2an|,an=2n-7,知bn=|log22n-7|=|n-7|,由此能求出数列{bn}的前n项和.
解答 解:(Ⅰ) 设正项等比数列{an}的公比为q,则q>0.
由已知S3=3a3+2a2有2a3+a2-a1=0,即$2{a_1}{q^2}+{a_1}q-{a_1}=0$,
∴2q2+q-1=0故$q=\frac{1}{2}$或q=-1(舍)
∴${a_n}={a_4}×{q^{n-4}}={({\frac{1}{2}})^{n-7}}$;
(Ⅱ)由(Ⅰ)知:bn=7-n故当n≤7时,bn≥0
∴当n≤7时,${T_n}={b_1}+{b_2}+…+{b_n}=\frac{{n({{b_1}+{b_n}})}}{2}=-\frac{n^2}{2}+\frac{13n}{2}$
当n>7时,Tn=b1+b2+…+b7-(b8+b9+…+bn)
=2(b1+b2+…+b7)-(b1+b2+…+bn)
=$\frac{{n}^{2}}{2}$-$\frac{13n}{2}$+42,
∴Tn=$\left\{\begin{array}{l}{-\frac{{n}^{2}}{2}+\frac{13n}{2}(0<n≤7)}\\{\frac{{n}^{2}}{2}-\frac{13n}{2}+42(n>7)}\end{array}\right.$.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
19.若△ABC的三个内角满足tanAtanBtanC>0,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 任意三角形 |
9.《算法统宗》是明朝程大位所著数学名著,其中有这样一段表述:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一”,其意大致为:有一七层宝塔,每层悬挂的红灯数为上一层的两倍,共有381盏灯,则塔从上至下的第三层有( )盏灯.
| A. | 14 | B. | 12 | C. | 8 | D. | 10 |
14.设f(x)=ex(sinx-cosx),其中 0≤x≤2011π,则 f(x)的极大值点个数是( )
| A. | 25 | B. | 1005 | C. | 26 | D. | 28 |
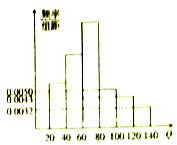 酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.如图为某市交管部门在一次夜间行动中依法查出的60名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中120≤Q<140人数包含Q≥140).
酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.如图为某市交管部门在一次夜间行动中依法查出的60名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中120≤Q<140人数包含Q≥140).