题目内容
13.若直线l:y=kx+1与圆C:x2+y2-2x-3=0交于A,B,则|AB|的最小值为$2\sqrt{2}$ .分析 判断直线l:y=kx+1恒过(0,1),在圆内,|AB|最小时,弦心距最大.计算弦心距,再求半弦长,由此能得出结论.
解答 解:圆C:x2+y2-2x-3=0可化为(x-1)2+y2=4,
∴圆心(1,0),半径r=2,
直线l:y=kx+1恒过(0,1),点(0,1)到圆心(1,0)的距离d=$\sqrt{2}$<2,
∴点(0,1)在圆内.
|AB|最小时,弦心距最大,最大为$\sqrt{2}$,
∴|AB|min=2$\sqrt{4-2}$=$2\sqrt{2}$,
故答案为:$2\sqrt{2}$.
点评 本题考查圆的简单性质的应用,考查学生分析解决问题的能力,确定|AB|最小时,弦心距最大是关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
3.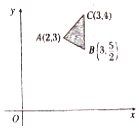 如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
 如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
如图,已知点(x,y)在△ABC所包围的阴影部分区域内(包含边界),若B(3,$\frac{5}{2}$)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )| A. | [-$\frac{1}{2}$,+∞) | B. | [0,+∞) | C. | (-∞,-$\frac{1}{2}$] | D. | [-$\frac{1}{2}$,0] |
18.已知回归直线的斜率为-1,样本点中心为(1,2),则回归直线方程为( )
| A. | $\widehat{y}$=x+3 | B. | $\widehat{y}$=-x+3 | C. | $\widehat{y}$=-x-3 | D. | $\widehat{y}$=-2x+4 |
2.如图,已知直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
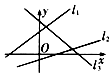

| A. | k1<k2<k3 | B. | k3<k2<k1 | C. | k1<k3<k2 | D. | k2<k1<k3 |
3.
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.

| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
