题目内容

14．当实数m为何值时，z=lg（m2-2m-2）+（m2+3m+2）i
（1）为实数       （2）为虚数     （3）对应的点在复平面的第二象限．

分析 （1）满足m2+3m+2=0，m2-2m-2＞0时，解得m即可得出；
（2）满足m2+3m+2≠0，m2-2m-2＞0时，解得m即可得出；
（3）满足0＜m2-2m-2＜1，m2+3m+2＞0时，解得m即可得出．

解答 解：（1）m2+3m+2=0，m2-2m-2＞0时，解得m=-1，-2，此时z为实数；
（2）m2+3m+2≠0，m2-2m-2＞0时，解得m＞$1+\sqrt{3}$，或m＜1-$\sqrt{3}$，且m≠-2时，此时z为虚数；
（3）0＜m2-2m-2＜1，m2+3m+2＞0时，解得1+$\sqrt{3}$＜m＜3，或$-1＜m＜1-\sqrt{3}$，此时对应的点在复平面的第二象限．

点评 本题考查了复数的有关概念及其几何意义、方程与不等式的解法，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
4．定义在R上的偶函数f（x），满足f（x+1）=-f（x），且f（x）在[-1，0]上是增函数，
①f（x）为周期函数；      
②f（x）的图象关于x=1对称；      
③f（x）在[0，1]上为增函数；
④f（x）在[1，2]上为减函数；   
⑤f（2）=f（0）．
则上述说法正确的有①②⑤．
5．（理科）如图，已知四棱锥P-ABCD的底面ABCD为菱形，且∠ABC=60°，AB=PC=2，PA=PB=$\sqrt{2}$，
（1）求证：平面PAB⊥平面ABCD；
（2）求二面角P-AC-B的余弦值．
2．已知数列{an}是首项为1，公比为$\frac{1}{2}$的等比数列，令Sn=a1+a2+…+an，Tn=a1（a1+a2+…+an）+a2（a2+a3+…+an）+…+an-1（an-1+an）+an2．若对一切正整数n，都有Tn＞c•Sn2，则c的取值范围是（-∞，$\frac{4}{3}$]．
9．对于函数f（x）=xex有以下命题：
①函数f（x）只有一个零点； 
②函数f（x）最小值为-e； 
③函数f（x）没有最大值； 
④函数f（x）在区间（-∞，0）上单调递减．
其中正确的命题是（只填序号）①③．
19．若数列{an}满足a1=1，a2=2，an=an-1+an-2（n∈N*，n＞2），则a6=（　　）
A．13B．8C．21D．10
6．已知函数f（x）=（x3-6x2+3x+t）ex，t∈R．
（1）若函数f（x）有三个极值点，求t的取值范围；
（2）若函数f（x）在x=a，x=b，x=c（a＜b＜c）处取得极值，且a+c=2b2，求f（x）的零点．
3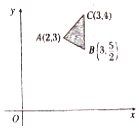．如图，已知点（x，y）在△ABC所包围的阴影部分区域内（包含边界），若B（3，$\frac{5}{2}$）是使得z=ax-y取得最大值的最优解，则实数a的取值范围为（　　）
A．[-$\frac{1}{2}$，+∞）B．[0，+∞）C．（-∞，-$\frac{1}{2}$]D．[-$\frac{1}{2}$，0]
4．设正项等比数列{an}的前n项和为Sn，且满足S3=3a3+2a2，a4=8．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列bn=log2an，求{|bn|}的前n项和Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网