题目内容
若sin（
+α）=
，则sin2（
-α）= ．
| π |
| 6 |
| 3 |
| 5 |
| π |
| 3 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知等式左边的角度变形后，利用诱导公式化简求出cos（
-α），再利用同角三角函数间的基本关系即可求出所求式子的值．
| π |
| 3 |
解答：
解：∵sin（
+α）=sin[
-（
-α）]=cos（
-α）=
，
∴sin2（
-α）=1-cos2（
-α）=1-
=
．
故答案为：
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 5 |
∴sin2（
| π |
| 3 |
| π |
| 3 |
| 9 |
| 25 |
| 16 |
| 25 |
故答案为：
| 16 |
| 25 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
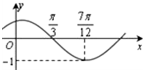函数f（x）=Asin（ωx+φ）的图象如图所示，为了得到g（x）=-Acosωx的图象，可以将f（x）的图象向右平移在数列{an}中，an+1=
（n∈N+）且a7=
，则a5=（ ）
| 2an |
| 2+an |
| 1 |
| 2 |
| A、1 | ||
B、
| ||
C、
| ||
| D、-1 |