题目内容
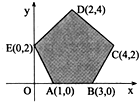已知以x，y为自变量的目标函数ω=kx+y（k＞0）的可行域如图阴影部分（含边界），若使ω取最大值时的最优解有无穷多个，则k的值为（ ）| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
考点：简单线性规划
专题：不等式的解法及应用
分析：根据目标函数的几何意义即可得到结论．
解答：
解：由ω=kx+y（k＞0），
得y=-kx+ω，（k＞0），
∵k＞0，∴直线的斜率-k＜0，
若使ω取最大值时的最优解有无穷多个，
则直线y=-kx+ω，和直线CD平行，
即-k=k CD=
=-1，
解得k=1，
故选：A
得y=-kx+ω，（k＞0），
∵k＞0，∴直线的斜率-k＜0，
若使ω取最大值时的最优解有无穷多个，
则直线y=-kx+ω，和直线CD平行，
即-k=k CD=
| 4-2 |
| 2-4 |
解得k=1，
故选：A
点评：本题主要考查线性规划的应用，根据目标函数的几何意义是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
设函数f（x）=cosωx（ω＞0），将f（x）的图象向右平移
个单位长度后，所得的图象与原图象重合，此时，记ω的最小值为ω0．若△ABC中三边a、b、c所对内角依次为A、B、C，且A=
，c2=a2+b2-
ab，则△ABC是（ ）
| π |
| 3 |
| ω0π |
| 18 |
| 3 |
| A、等边三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
函数f（x）=3x+log2x的零点所在区间为（ ）
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
下列命题中，正确的是（ ）
| A、两个平面同垂直于一个平面，则此二平面平行 |
| B、同垂直于两个平行平面的两个平面平行 |
| C、同垂直于两条平行直线的两个平面平行 |
| D、同垂直于一条直线的两个平面不一定平行 |