题目内容
设函数f(x)=2x-cosx,{an}是公差为
的等差数列,f(a1)+f(a2)+f(a3)=3π,则f(a1)+f(a2)+…f(a10)= .
| π |
| 4 |
考点:数列与函数的综合
专题:等差数列与等比数列
分析:由已知得an=a1+(n-1)•
,f(a1)+f(a2)+f(a3)=6a1+
-cos(a1+
)=3π,从而an=
.由此能求出f(a1)+f(a2)+…f(a10)的值.
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
| nπ |
| 4 |
解答:
解:∵{an}是公差为
的等差数列,
∴an=a1+(n-1)•
,
∵函数f(x)=2x-cosx,f(a1)+f(a2)+f(a3)=3π,
∴f(a1)+f(a2)+f(a3)=2a1-cosa1+2(a1+
)-cos(a1+
)+2(a1+
)-cos(a1+
)
=6a1+
-cos(a1+
)=3π,
解得a1=
,即an=
.
∴f(a1)+f(a2)+…f(a10)
=2(
+
+…+
)-(cos
+cos
+…+cos
)
=
×10×(10+1)×
-cos
=
-
.
故答案为:
-
.
| π |
| 4 |
∴an=a1+(n-1)•
| π |
| 4 |
∵函数f(x)=2x-cosx,f(a1)+f(a2)+f(a3)=3π,
∴f(a1)+f(a2)+f(a3)=2a1-cosa1+2(a1+
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
=6a1+
| 3π |
| 2 |
| π |
| 4 |
解得a1=
| π |
| 4 |
| nπ |
| 4 |
∴f(a1)+f(a2)+…f(a10)
=2(
| π |
| 4 |
| 2π |
| 4 |
| 10π |
| 4 |
| π |
| 4 |
| 2π |
| 4 |
| 10π |
| 4 |
=
| π |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
=
| 55π |
| 2 |
| ||
| 2 |
故答案为:
| 55π |
| 2 |
| ||
| 2 |
点评:本题考查函数值的求法,是中档题,解题时要注意数列性质、三角函数知识的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数y=
cos(x+
)的图象为C,为了得到函数y=
cos(x-
)的图象只需把C上所有的点( )
| 1 |
| 3 |
| π |
| 7 |
| 1 |
| 3 |
| π |
| 7 |
A、向右平行移动
| ||
B、向左平行移动
| ||
C、向右平行移动
| ||
D、向左平行移动
|
如果a>b>0,则下列不等式成立的是( )
①
<
; ②a3>b3;③lg(a2+1)>lg(b2+1);④2a>2b.
①
| 1 |
| a |
| 1 |
| b |
| A、①②③④ | B、①②③ |
| C、①② | D、③④ |
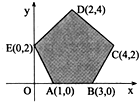 已知以x,y为自变量的目标函数ω=kx+y(k>0)的可行域如图阴影部分(含边界),若使ω取最大值时的最优解有无穷多个,则k的值为( )
已知以x,y为自变量的目标函数ω=kx+y(k>0)的可行域如图阴影部分(含边界),若使ω取最大值时的最优解有无穷多个,则k的值为( )