题目内容
设函数f（x）=cosωx（ω＞0），将f（x）的图象向右平移
个单位长度后，所得的图象与原图象重合，此时，记ω的最小值为ω0．若△ABC中三边a、b、c所对内角依次为A、B、C，且A=
，c2=a2+b2-
ab，则△ABC是（ ）
| π |
| 3 |
| ω0π |
| 18 |
| 3 |
| A、等边三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
考点：函数y=Asin（ωx+φ）的图象变换,余弦定理
专题：三角函数的图像与性质
分析：由题意易得
=n×
，n∈Z，可得ω0=6，进而可得A=
，再由余弦定理可得cosC=
，可得C=
，可得B值，可判三角形形状．
| π |
| 3 |
| 2π |
| ω |
| π |
| 3 |
| ||
| 2 |
| π |
| 6 |
解答：
解：∵f（x）=cosωx（ω＞0）的图象向右平移
个单位长度后所得的图象与原图象重合，
∴
=n×
，n∈Z，∴ω=6n，又ω＞0，∴ω的最小值为ω0=6，
∴A=
=
，∵c2=a2+b2-
ab，
∴由余弦定理可得cosC=
=
，∴C=
，
∴B=π-A-C=
，即△ABC为直角三角形
故选：D
| π |
| 3 |
∴
| π |
| 3 |
| 2π |
| ω |
∴A=
| ω0π |
| 18 |
| π |
| 3 |
| 3 |
∴由余弦定理可得cosC=
| a2+b2-c2 |
| 2ab |
| ||
| 2 |
| π |
| 6 |
∴B=π-A-C=
| π |
| 2 |
故选：D
点评：本题考查三角函数的图象的性质，涉及余弦定理的应用，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知角α终边上一点P（
，1），则2sin2α-3tanα=（ ）
| 3 |
A、-1-3
| ||
B、1-3
| ||
C、-2
| ||
| D、0 |
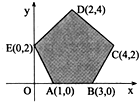已知以x，y为自变量的目标函数ω=kx+y（k＞0）的可行域如图阴影部分（含边界），若使ω取最大值时的最优解有无穷多个，则k的值为（ ）