题目内容
“a=b-4”是“直线y=x+2与圆(x-a)2+(y-b)2=2相切”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:直线与圆,简易逻辑
分析:根据充分条件和必要条件的定义结合直线和圆相切的条件进行判断即可.
解答:
解:若直线y=x+2与圆(x-a)2+(y-b)2=2相切,
则圆心坐标为(a,b),半径R=
,
圆心到直线的距离d=
=
,
即|a-b+2|=2,
解得a-b+2=2或a-b+2=-2,
即a=b或a=b-4,
故“a=b-4”是“直线y=x+2与圆(x-a)2+(y-b)2=2相切”的充分不必要条件,
故选:A
则圆心坐标为(a,b),半径R=
| 2 |
圆心到直线的距离d=
| |a-b+2| | ||
|
| 2 |
即|a-b+2|=2,
解得a-b+2=2或a-b+2=-2,
即a=b或a=b-4,
故“a=b-4”是“直线y=x+2与圆(x-a)2+(y-b)2=2相切”的充分不必要条件,
故选:A
点评:本题主要考查充分条件和必要条件的判断,根据直线和圆相切的条件是解决本题的关键.

练习册系列答案
相关题目
若cos(
-α)=
,α∈(-π,0),则sin(
+2α)=( )
| π |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
“A=∅”是“A∪B=B”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |
若a∈R,则“a=2”是“(a-2)(a+4)=0”的( )
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
若直线y=1的倾斜角为α,则α等于( )
| A、0° | B、45° |
| C、90° | D、不存在 |
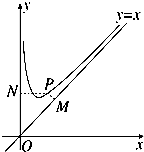 如图,函数f(x)=x+
如图,函数f(x)=x+