题目内容
 函数y=f(x)的导函数f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )
函数y=f(x)的导函数f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )A、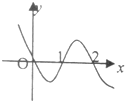 |
B、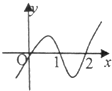 |
C、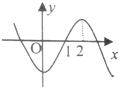 |
D、 |
考点:函数的单调性与导数的关系
专题:函数的性质及应用
分析:根据导函数f′(x)的正负与函数y=f(x)的单调性关系,结合图象即可得出答案.
解答:
解:根据函数y=f(x)的导函数f′(x)的图象知,
当x<0时,f′(x)<0,∴f(x)是减函数;
当0<x<2时,f′(x)>0,∴f(x)是增函数;
当x>2时,f′(x)<0,∴f(x)是减函数;
∴满足以上条件的应是C.
故选:C.
当x<0时,f′(x)<0,∴f(x)是减函数;
当0<x<2时,f′(x)>0,∴f(x)是增函数;
当x>2时,f′(x)<0,∴f(x)是减函数;
∴满足以上条件的应是C.
故选:C.
点评:本题考查了函数的图象与性质的应用问题,解题时应结合函数与它的导函数的关系,进行判定函数的单调性,是基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 如图,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=100米,点C位于BD上,则山高AB等于( )
如图,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=100米,点C位于BD上,则山高AB等于( )| A、100米 | ||
B、50
| ||
C、50
| ||
D、50(
|
在平面坐标系xOy中,抛物线y2=2px的焦点F与椭圆
+
=1的左焦点重合,点A在抛物线上,且|AF|=4,若P是抛物线准线上一动点,则|PO|+|PA|的最小值为( )
| x2 |
| 6 |
| y2 |
| 2 |
| A、6 | ||
B、2+4
| ||
C、2
| ||
D、4+2
|
三角形ABC中,∠C=90°,AB=2,AC=1,若
=
,则
•
=( )
| AD |
| 3 |
| 2 |
| AB |
| CD |
| CB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,A,B,C所对边分别为a,b,c,则下列各式中一定成立的是( )
A、
| ||||
B、
| ||||
| C、asinB=bcosA | ||||
| D、a=2RcosA |