题目内容
20.若f(x)=x2-2(a-1)x+2在(-∞,3]上是减函数,则a的取值范围是[4,+∞).分析 根据一元二次函数单调性的性质进行求解即可.
解答 解:若f(x)=x2-2(a-1)x+2在(-∞,3]上是减函数,
则函数的对称轴x=$-\frac{-2(a-1)}{2}$=a-1≥3,
即a≥4,
故答案为:[4,+∞);
点评 本题主要考查函数单调性的应用,根据一元二次函数单调性的性质建立对称轴和单调区间的关系是解决本题的关键.

练习册系列答案
相关题目
11.已知关于x的二次函数f(x)=ax2-4bx+1,设集合A={-1,1,2,3,4,5},B={-2,-1,1,2,3,4},分别从集合A和B中随机取一个数记为a和b,则函数y=f(x)在[1,+∞)上单调递增的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{9}$ |
9.已知函数f(x)=x2+a(b+1)x+a+b(a,b∈R),则“a=0”是“f(x)为偶函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
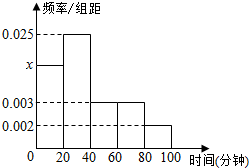 某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动
某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动