题目内容
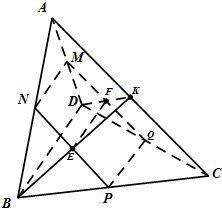 三棱锥A-BCD中,ABD,BCD都是边长为2的等边三角形,且平面ABD⊥平面BCD,设M,N,P,Q分别为线段AD,AB,BC,CD的中点.
三棱锥A-BCD中,ABD,BCD都是边长为2的等边三角形,且平面ABD⊥平面BCD,设M,N,P,Q分别为线段AD,AB,BC,CD的中点.(1)证明:四边形MNPQ是矩形;
(2)求二面角A-NP-M的余弦值.
考点:二面角的平面角及求法
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)运用中位线定理,证得四边形MNPQ为平行四边形,再取BD的中点H,连接AH,CH,运用等边三角形的性质和线面垂直的判定定理,即可得证;
(2)取AC的中点为K,连接BK,交NP于E,连接DK,交MQ于F,连接EF,由EF⊥NP,EK⊥NP证得∠FEK均为二面角A-NP-M的平面角,再由等边三角形和面面垂直的性质,计算出EF,EK,FK,由余弦定理即可得到结果.
(2)取AC的中点为K,连接BK,交NP于E,连接DK,交MQ于F,连接EF,由EF⊥NP,EK⊥NP证得∠FEK均为二面角A-NP-M的平面角,再由等边三角形和面面垂直的性质,计算出EF,EK,FK,由余弦定理即可得到结果.
解答:
 (1)证明由于M,N为AD,AB的中点,
(1)证明由于M,N为AD,AB的中点,
则MN∥BD,MN=
BD,
由于P,Q为CB,CD的中点,
则PQ∥BD,PQ=
BD,
即有MN∥PQ,且MN=PQ,
则四边形MNPQ为平行四边形,
取BD的中点H,连接AH,CH,
由于三角形ABD和三角形CBD均为等边三角形,
则AH⊥BD,CH⊥BD,
则BD⊥平面ACH,则BD⊥AC,
则由MN∥BD,MQ∥AC,
则MN⊥MQ,则四边形MNPQ为矩形;
(2)解:取AC的中点为K,连接BK,交NP于E,
连接DK,交MQ于F,连接EF,
由于AB=BC,则EK⊥NP,DK⊥AC,
则BD∥EF,EF⊥NP,
则有∠FEK均为二面角A-NP-M的平面角,
由E,F为中点,则EK=FK=
BK=
DK,
由于平面ABD⊥平面BCD,则由(1)知,AH⊥BD,
得到AH⊥平面BCD,则AH⊥CH,
则由ABD,BCD都是边长为2的等边三角形,
即有AH=CH=
,AC=
,BK=DK=
=
,
则在三角形EFK中,EF=1,EK=FK=
BK=
,
则cos∠FEK=
=
.
 (1)证明由于M,N为AD,AB的中点,
(1)证明由于M,N为AD,AB的中点,则MN∥BD,MN=
| 1 |
| 2 |
由于P,Q为CB,CD的中点,
则PQ∥BD,PQ=
| 1 |
| 2 |
即有MN∥PQ,且MN=PQ,
则四边形MNPQ为平行四边形,
取BD的中点H,连接AH,CH,
由于三角形ABD和三角形CBD均为等边三角形,
则AH⊥BD,CH⊥BD,
则BD⊥平面ACH,则BD⊥AC,
则由MN∥BD,MQ∥AC,
则MN⊥MQ,则四边形MNPQ为矩形;
(2)解:取AC的中点为K,连接BK,交NP于E,
连接DK,交MQ于F,连接EF,
由于AB=BC,则EK⊥NP,DK⊥AC,
则BD∥EF,EF⊥NP,
则有∠FEK均为二面角A-NP-M的平面角,
由E,F为中点,则EK=FK=
| 1 |
| 2 |
| 1 |
| 2 |
由于平面ABD⊥平面BCD,则由(1)知,AH⊥BD,
得到AH⊥平面BCD,则AH⊥CH,
则由ABD,BCD都是边长为2的等边三角形,
即有AH=CH=
| 3 |
| 6 |
4-
|
| ||
| 2 |
则在三角形EFK中,EF=1,EK=FK=
| 1 |
| 2 |
| ||
| 4 |
则cos∠FEK=
1+
| ||||
2×1×
|
| ||
| 5 |
点评:本题考查空间直线与平面垂直的判断和性质定理及运用,考查面面垂直的性质定理,以及空间二面角的求法,考查蕴算能力,属于中档题.

练习册系列答案
相关题目
