题目内容
已知f(x)=(
)|x|,定义函数:g(x)=
(1)画出函数g(x)的图象并写出其单调区间;
(2)设t∈R,若关于t的方程g(t)=-a2+4a-3有解,求实数a的取值范围;
(3)若m∈R,且f(mx-1)>(
)x对x∈[2,3]恒成立,求m的取值范围.
| 1 |
| 2 |
|
(1)画出函数g(x)的图象并写出其单调区间;
(2)设t∈R,若关于t的方程g(t)=-a2+4a-3有解,求实数a的取值范围;
(3)若m∈R,且f(mx-1)>(
| 1 |
| 2 |
考点:函数恒成立问题,分段函数的应用
专题:函数的性质及应用
分析:(1)由已知结合指数函数的图象作出函数g(x)的图象并写出其单调区间;
(2)由(1)知g(t)的范围,求解不等式0<-a2+4a-3≤
得答案;
(3)求出(
)x在x∈[2,3]上的范围,然后分m<0和m≥0把f(mx-1)>(
)x对x∈[2,3]恒成立转化为指数不等式,求出m的范围,取并集后得答案.
(2)由(1)知g(t)的范围,求解不等式0<-a2+4a-3≤
| 1 |
| 2 |
(3)求出(
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)f(x)=(
)|x|,则函数g(x)=
的图象如图,
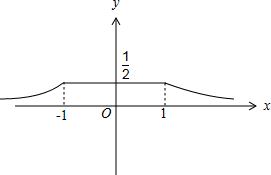
增区间(-∞,-1),减区间(1,+∞);
(2)由(1)知,函数g(t)的值域为(0,
],
由0<-a2+4a-3≤
,解得1<a≤
或
≤a<3.
(3)当x∈[2,3],(
)x∈[
,
],
要使f(mx-1)>(
)x对x∈[2,3]恒成立,
则当m<0时,(
)|mx-1|>
,得|mx-1|<2,
解得-
<m<0,
∴-
<m<0;
当m≥0时,(
)|mx-1|>
,得|mx-1|<3,
解得0≤m<
,
∴0≤m<
.
综上,m的取值范围是-
<m<
.
| 1 |
| 2 |
|

增区间(-∞,-1),减区间(1,+∞);
(2)由(1)知,函数g(t)的值域为(0,
| 1 |
| 2 |
由0<-a2+4a-3≤
| 1 |
| 2 |
4-
| ||
| 2 |
4+
| ||
| 2 |
(3)当x∈[2,3],(
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
要使f(mx-1)>(
| 1 |
| 2 |
则当m<0时,(
| 1 |
| 2 |
| 1 |
| 4 |
解得-
| 1 |
| x |
∴-
| 1 |
| 2 |
当m≥0时,(
| 1 |
| 2 |
| 1 |
| 8 |
解得0≤m<
| 4 |
| x |
∴0≤m<
| 4 |
| 3 |
综上,m的取值范围是-
| 1 |
| 2 |
| 4 |
| 3 |
点评:本题考查了函数恒成立问题,考查了分段函数的应用,体现了数学转化思想方法,是中档题.

练习册系列答案
相关题目
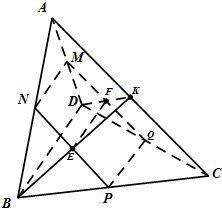 三棱锥A-BCD中,ABD,BCD都是边长为2的等边三角形,且平面ABD⊥平面BCD,设M,N,P,Q分别为线段AD,AB,BC,CD的中点.
三棱锥A-BCD中,ABD,BCD都是边长为2的等边三角形,且平面ABD⊥平面BCD,设M,N,P,Q分别为线段AD,AB,BC,CD的中点.