题目内容
已知函数f(x)=|x-a|,若f(x)<m的解集为{x|-1≤x≤5},其中a、m为实数,则a+m= .
考点:绝对值不等式的解法
专题:不等式
分析:由|x-a|<m,得:-m<x-a<m,然后解答即可.
解答:
解:由题意可得:m>0,
∵|x-a|<m,
解得:-m<x-a<m,
即a-m<x<a+m,
又f(x)<m的解集为{x|-1≤x≤5},
∴
,
∴a+m=5.
故答案为:5
∵|x-a|<m,
解得:-m<x-a<m,
即a-m<x<a+m,
又f(x)<m的解集为{x|-1≤x≤5},
∴
|
∴a+m=5.
故答案为:5
点评:本题主要考查绝对值不等式的性质,属于基础题

练习册系列答案
相关题目
下面式子中,
①
=3-π;
②无理数e是自然对数的底数,可以得 logπ1+lne=1;
③若a>b,则 a2>b2;
④若a>b,则(
)a<(
)b
正确的个数有( )
①
| 4 | (3-π)4 |
②无理数e是自然对数的底数,可以得 logπ1+lne=1;
③若a>b,则 a2>b2;
④若a>b,则(
| 1 |
| 3 |
| 1 |
| 3 |
正确的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
若圆柱与圆锥的高相等,且轴截面面积也相等,那么圆柱与圆锥的体积之比为( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
设α,β为两个不重合的平面,m,n为两条不重合的直线,则下列命题中正确的是( )
| A、若m⊥n,m⊥α则n∥α |
| B、若α⊥β,α∩β=m,n?α,n⊥m,则n⊥β |
| C、若m⊥n,m∥α,n∥β,则α⊥β |
| D、若n?α,m?β,α与β相交且不垂直,则n与m不垂直 |
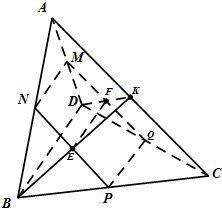 三棱锥A-BCD中,ABD,BCD都是边长为2的等边三角形,且平面ABD⊥平面BCD,设M,N,P,Q分别为线段AD,AB,BC,CD的中点.
三棱锥A-BCD中,ABD,BCD都是边长为2的等边三角形,且平面ABD⊥平面BCD,设M,N,P,Q分别为线段AD,AB,BC,CD的中点.