题目内容
用十字相乘法分解因式：ax2+（1-4a）x-4=0．
考点：因式分解定理
专题：计算题
分析：由ax2+（1-4a）x-4=0．用“十字相乘法”分解因式可得（ax+1）（x-4）=0．对a分类讨论即可解出．
解答：
解：由ax2+（1-4a）x-4=0．可得（ax+1）（x-4）=0．
当a=0时，方程化为x-4=0，解得x=4．
当a≠0时，方程化为(x+
)（x-4）=0，解得x=4或-
．
当a=0时，方程化为x-4=0，解得x=4．
当a≠0时，方程化为(x+
| 1 |
| a |
| 1 |
| a |
点评：本题考查了用“十字相乘法”分解因式解方程，属于基础题．
练习册系列答案
相关题目
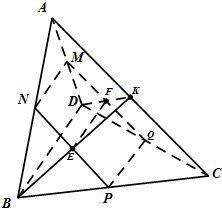三棱锥A-BCD中，ABD，BCD都是边长为2的等边三角形，且平面ABD⊥平面BCD，设M，N，P，Q分别为线段AD，AB，BC，CD的中点．