题目内容
已知函数y=2sin(
x-
)
(1)画出函数的简图;
(2)写出函数的单调减区间.
| 1 |
| 3 |
| π |
| 3 |
(1)画出函数的简图;
(2)写出函数的单调减区间.
考点:复合三角函数的单调性
专题:作图题,函数的性质及应用,三角函数的图像与性质
分析:(1)根据“五点法”作图的步骤,我们令相位角
x-
分别等0,
,π,
,2π,并求出对应的x,y值,描出五点后,用平滑曲线连接后,即可得到函数 y=2sin(
x-
)的一个周期简图;
(2)利用正弦函数的单调减区间,求出f(x)的单调减区间.
| 1 |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
| 1 |
| 3 |
| π |
| 3 |
(2)利用正弦函数的单调减区间,求出f(x)的单调减区间.
解答:
解:(1)列表如下:
描点连线可得一个周期内的简图.再由周期性向左(右)平移6π的整数倍,可得在R上的图象.
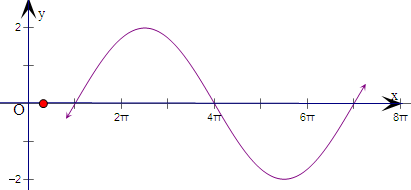
(2)令2kπ+
≤
x-
≤2kπ+
,k∈Z,
解得6kπ+
≤x≤6kπ+
,k∈Z,
则所求的单调减区间为[6kπ+
,6kπ+
],k∈Z.
| x | π |
| 4π |
| 7π | ||||||||
| 0 |
| π |
| 2π | ||||||||
| y | 0 | 2 | 0 | -2 | 0 |

(2)令2kπ+
| π |
| 2 |
| 1 |
| 3 |
| π |
| 3 |
| 3π |
| 2 |
解得6kπ+
| 5π |
| 2 |
| 11π |
| 2 |
则所求的单调减区间为[6kπ+
| 5π |
| 2 |
| 11π |
| 2 |
点评:本题考查的知识点是五点法作函数y=Asin(ωx+φ)的图象,函数y=Asin(ωx+φ)的振幅,频率,单调区间,初相等性质.其中利用“五点法”画出函数的简图,并根据复合三角函数的单调性作答是解答本题的关键.

练习册系列答案
相关题目
若实数x,y满足约束条件
,则2x+y的最大值是( )
|
A、
| ||
| B、3 | ||
| C、-2 | ||
| D、2 |
若双曲线
+
=1的离心率为
,则实数k的值为( )
| x2 |
| 3 |
| y2 |
| k |
| 3 |
A、-
| ||
B、
| ||
| C、-6 | ||
| D、6 |
运行如图所示的程序框图,则输出的所有实数对(x,y)所对应的点都在函数( )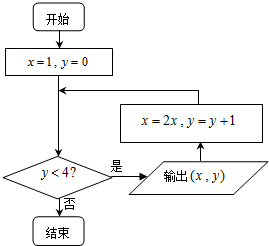

| A、y=x-1的图象上 | ||
B、y=
| ||
| C、y=2x-1-1的图象上 | ||
| D、y=log2x的图象上 |