题目内容
13.平行四边形ABCD中,AB=3,AD=2,∠BAD=120°,P是平行四边形ABCD内一点,且AP=1,若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}$,则3x+2y的最大值为2.分析 根据$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}$,得出${\overrightarrow{AP}}^{2}$=1,利用基本不等式得出3x+2y的最大值.
解答 解:∵$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}$,
∴${\overrightarrow{AP}}^{2}$=${(x\overrightarrow{AB}+y\overrightarrow{AD})}^{2}$=9x2+4y2+2xy×3×2×(-$\frac{1}{2}$)
=(3x+2y)2-3•3x•2y≥(3x+2y)2-$\frac{3}{4}$×(3x+2y)2
=$\frac{1}{4}$×(3x+2y)2;
又${|\overrightarrow{AP}|}^{2}$=1,
即$\frac{1}{4}$×(3x+2y)2≤1,
所以3x+2y≤2,当且仅当3x=2y,
即x=$\frac{1}{3}$,y=$\frac{1}{2}$时,
3x+2y取得最大值2.
故答案为:2.
点评 本题考查了平面向量的数量积与模长的应用问题,也考查了基本不等式的应用问题,是基础题目.

练习册系列答案
相关题目
3.在正方体ABCD-A1B1C1D1中,异面直线A1B与AD1所成角的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
4.在平面直角坐标系xOy中,圆C的方程为x2+y2-8x+15=0,若直线y=kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | 3 |
1.将函数y=sin(2x+$\frac{π}{6}$)的图象向左平移$\frac{π}{3}$个单位,所得函数的解析式为( )
| A. | $y=sin({2x+\frac{5π}{6}})$ | B. | y=-cos2x | C. | y=cos2x | D. | $y=sin({2x-\frac{π}{6}})$ |
8.函数y=ln|x|-x2的图象大致为( )
| A. | 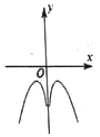 | B. | 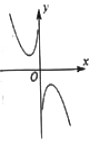 | C. |  | D. | 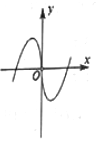 |
5.已知双曲线$\frac{{x}^{2}}{m}$-y2=1的一个焦点与抛物线y2=8x焦点相同,则此双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{2\sqrt{15}}{15}$ |