题目内容
若椭圆
+
=1(a>b>0)与曲线x2+y2=a2-b2恒有公共点,则椭圆离心率e的取值范围是 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先根据圆的方程可推断出圆与椭圆相切或相交,进而推断出b≤c,利用a,b和c的关系求得a和c的不等式关系,进而求得e的范围.
解答:
解:根据题意可知圆与椭圆相切或相交,
∴b≤c,
∴b2≤c2,
∴a2≤2c2,
∵a>0,c>0,
∴e2≥
∴e≥
,
又由椭圆的离心率小于1,可得
≤e<1,
故答案为:
≤e<1
∴b≤c,
∴b2≤c2,
∴a2≤2c2,
∵a>0,c>0,
∴e2≥
| 1 |
| 2 |
∴e≥
| ||
| 2 |
又由椭圆的离心率小于1,可得
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题主要考查了椭圆的简单性质和椭圆与圆的关系.考查了学生综合分析问题的能力和数形结合思想的运用.

练习册系列答案
相关题目
根据如下样本数据:
得到的回归方程为
=
x+
,则( )
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 | -3 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等式x2+2x<
+
对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是( )
| a |
| b |
| 16b |
| a |
| A、hmax(x) |
| B、(-∞,-2)∪(0,+∞) |
| C、(-4,2) |
| D、(-∞,-4)∪(2,+∞) |
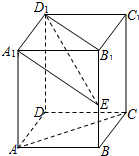 如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为
如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为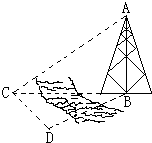 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40(米),并在点C测得塔顶A的仰角为30°.则塔高AB=
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=75°,∠BDC=60°,CD=40(米),并在点C测得塔顶A的仰角为30°.则塔高AB=