题目内容
17.已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<$\frac{π}{2}$)的图象与x轴的交点中,相邻两个交点之间的距离为$\frac{π}{2}$,且图象上一个最低点为$M(\frac{2π}{3},-2)$(1)求A,ω,φ的值.
(2)写出函数f(x)图象的对称中心及单调递增区间.
(3)当x∈$[{\frac{π}{12},\frac{π}{2}}]$时,求f(x)的值域.
分析 (1)由题意知,A=2,T=π,可求得ω,由图象上一个最低点为$M(\frac{2π}{3},-2)$,可求得φ;
(2)求f(x)的解析式,根据正弦函数的图象与性质,写出函数f(x)图象的对称中心及单调递增区间;
(3)由x∈$[{\frac{π}{12},\frac{π}{2}}]$⇒2x+$\frac{π}{6}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],利用正弦函数的单调性即可求得f(x)的值域.
解答 解:(1)由题意知,A=2,T=π,∴ω=2;
又图象上一个最低点为$M(\frac{2π}{3},-2)$,
∴2×$\frac{2π}{3}$+φ=2kπ-$\frac{π}{2}$,k∈Z,
∵0<φ<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$;
(2)f(x)=2sin(2x+$\frac{π}{6}$),令2x+$\frac{π}{6}$=kπ,可得x=$\frac{kπ}{2}-\frac{π}{12}$,
∴函数f(x)图象的对称中心为($\frac{kπ}{2}-\frac{π}{12}$,0),k∈Z;
由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$2kπ+$\frac{π}{2}$(k∈Z)得f(x)的单调递增区间为$[-\frac{π}{3}+kπ,\frac{π}{6}+kπ]$,k∈Z;
(3)∵x∈$[{\frac{π}{12},\frac{π}{2}}]$,
∴2x+$\frac{π}{6}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],
∴-$\frac{1}{2}$≤sin(2x+$\frac{π}{6}$)≤1,
∴-1≤f(x)≤2.
即f(x)的值域为[-1,2].
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的单调性与最值,属于中档题.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| 拼图数x/个 | 10 | 20 | 30 | 40 | 50 |
| 加工时间y/分钟 | 62 | 68 | 75 | 81 | 89 |
(2)求回归方程;
(3)根据求出的回归方程,预测加工2 00个拼图需用多少分钟.
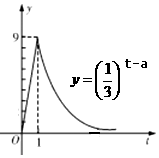 我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.