题目内容
18.已知集合P={-1,0,1},$Q=\left\{{x\left|{y=\sqrt{x+1}}\right.}\right\}$,则P∩Q=( )| A. | P | B. | Q | C. | {-1,1} | D. | {0,1} |
分析 先分别求出集合P和Q,由此利用交集定义能出P∩Q.
解答 解:∵集合P={-1,0,1},
$Q=\left\{{x\left|{y=\sqrt{x+1}}\right.}\right\}$={x|x≥-1},
∴P∩Q={-1,0,1}=P.
故选:A.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
相关题目
7.为迎接春节,某工厂大批生产小孩玩具--拼图,工厂为了规定工时定额,需要确定加工拼图所花费的时间,为此进行了5次试验,测得的数据如下:
(1)画出散点图,并判断y与x是否具有相关关系;
(2)求回归方程;
(3)根据求出的回归方程,预测加工2 00个拼图需用多少分钟.
| 拼图数x/个 | 10 | 20 | 30 | 40 | 50 |
| 加工时间y/分钟 | 62 | 68 | 75 | 81 | 89 |
(2)求回归方程;
(3)根据求出的回归方程,预测加工2 00个拼图需用多少分钟.
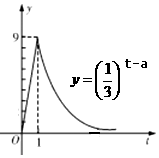 我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线. 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.