题目内容
17.已知△ABC为非直角三角形,其内角A、B、C的对边分别为a、b、c,且有$\sqrt{3}$sin$\frac{C}{2}co{s}^{2}\frac{B}{2}-cos$$\frac{C}{2}$cos2$\frac{B}{2}-\frac{\sqrt{3}}{2}sin\frac{C}{2}+\frac{1}{2}cos\frac{C}{2}$=0.(1)求角C;
(2)若c=3,sinB=3sinA,求a,b的值.
分析 (1)利用二倍角公式与和差公式对已知条件左侧分解因式,得出C.
(2)利用正余弦定理得出a,b的关系,连理方程组解出a,b.
解答 解:(1)∵$\sqrt{3}$sin$\frac{C}{2}co{s}^{2}\frac{B}{2}-cos$$\frac{C}{2}$cos2$\frac{B}{2}-\frac{\sqrt{3}}{2}sin\frac{C}{2}+\frac{1}{2}cos\frac{C}{2}$=0.
∴cos2$\frac{B}{2}$($\sqrt{3}$sin$\frac{C}{2}$-cos$\frac{C}{2}$)-$\frac{\sqrt{3}}{2}$sin$\frac{C}{2}$+$\frac{1}{2}$cos$\frac{C}{2}$=0.
∴cos2$\frac{B}{2}$•2sin($\frac{C}{2}-\frac{π}{6}$)-sin($\frac{C}{2}$-$\frac{π}{6}$)-0,
∴sin($\frac{C}{2}$-$\frac{π}{6}$)(2cos2$\frac{B}{2}$-1)=0,
∴sin($\frac{C}{2}-\frac{π}{6}$)cosB=0,
∴sin($\frac{C}{2}-\frac{π}{6}$)=0或cosB=0.
∴$\frac{C}{2}-\frac{π}{6}$=kπ或B=$\frac{π}{2}$(舍去).
∴C=2kπ+$\frac{π}{3}$,k∈Z.
∴C=$\frac{π}{3}$.
(2)若sinB=3sinA,则由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$,得b=3a,①
又∵c=3,则由余弦定理,得9=a2+b2-2abcos$\frac{π}{3}$,②
联立方程①②,解得a=$\frac{3\sqrt{7}}{7}$,b=$\frac{9\sqrt{7}}{7}$.
点评 本题考查了三角函数的恒等变换,正余弦定理在解三角形中的应用,属于中档题.

| A. | 2sinx | B. | 2cosx | C. | -2sinx | D. | -2cosx |
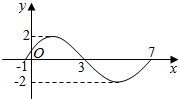 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )| A. | 2sin($\frac{x}{4}$-$\frac{π}{4}$) | B. | 2sin($\frac{x}{4}$+$\frac{π}{4}$) | C. | 2sin($\frac{πx}{4}$-$\frac{π}{4}$) | D. | 2sin($\frac{πx}{4}$+$\frac{π}{4}$) |
| A. | [$-\frac{3}{8}$+k,$\frac{1}{8}$+k](k∈Z) | B. | (-$\frac{1}{8}$+k,$\frac{1}{8}$+k](k∈Z) | C. | [$-\frac{3}{8}$+k,$\frac{1}{8}$+k](k∈Z) | D. | [$\frac{1}{8}$+k,$\frac{3}{8}$+k)(k∈Z) |
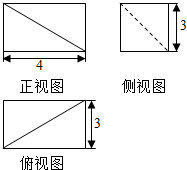
| A. | 45 | B. | 36 | C. | 30 | D. | 6 |