题目内容
2.函数y=$lo{g}_{\frac{1}{2}}sin(2πx+\frac{π}{4})$的单调递减区间是( )| A. | [$-\frac{3}{8}$+k,$\frac{1}{8}$+k](k∈Z) | B. | (-$\frac{1}{8}$+k,$\frac{1}{8}$+k](k∈Z) | C. | [$-\frac{3}{8}$+k,$\frac{1}{8}$+k](k∈Z) | D. | [$\frac{1}{8}$+k,$\frac{3}{8}$+k)(k∈Z) |
分析 根据复合函数单调性之间的关系,进行求解即可.
解答 解:要求函数y=$lo{g}_{\frac{1}{2}}sin(2πx+\frac{π}{4})$的单调递减区间,即求出函数y=sin(2πx+$\frac{π}{4}$)的单调递增区间且sin(2πx+$\frac{π}{4}$)>0,
即2kπ<2πx+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z,
即-$\frac{1}{8}$+k<x≤$\frac{1}{8}$+k,
即函数的单调递减区间为(-$\frac{1}{8}$+k,$\frac{1}{8}$+k].
故选:B
点评 本题主要考查函数单调区间的求解,利用复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
10.已知M是椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{16}$=1上的点,若F1,F2是椭圆的两个焦点,则|MF1|+|MF2|=( )
| A. | 6 | B. | 8 | C. | 18 | D. | 32 |
14.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$经过一、三象限的渐近线为m,若圆${x^2}+{y^2}-2\sqrt{5}x-2\sqrt{5}y+6=0$上至少有三个不同的点到m的距离为1,则此双曲线的离心率e的取值范围为( )
| A. | $[{\frac{{\sqrt{5}}}{2},2\sqrt{5}}]$ | B. | $({1,\sqrt{5}}]$ | C. | $[{\frac{{\sqrt{5}}}{2},\sqrt{5}}]$ | D. | $[{\sqrt{5},2\sqrt{5}}]$ |
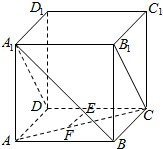 如图,正方体ABCD-A1B1C1D1中,E是A1B上的点,F是AC上的点,且A1E=2EB,CF=2AF.求证:EF∥平面A1B1CD.
如图,正方体ABCD-A1B1C1D1中,E是A1B上的点,F是AC上的点,且A1E=2EB,CF=2AF.求证:EF∥平面A1B1CD.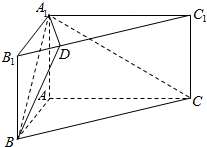 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,$AC=2\sqrt{3}$,$A{A_1}=\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,$AC=2\sqrt{3}$,$A{A_1}=\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D.