题目内容
12.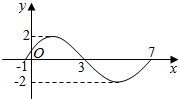 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,如图所示,则f(x)的解析式为( )| A. | 2sin($\frac{x}{4}$-$\frac{π}{4}$) | B. | 2sin($\frac{x}{4}$+$\frac{π}{4}$) | C. | 2sin($\frac{πx}{4}$-$\frac{π}{4}$) | D. | 2sin($\frac{πx}{4}$+$\frac{π}{4}$) |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
解答 解:由函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一个周期的图象,
可得A=2,$\frac{2π}{ω}$=7+1=8,∴ω=$\frac{π}{4}$.
再根据五点法作图可得,$\frac{π}{4}$•(-1)+φ=0,求得φ=$\frac{π}{4}$,
∴函数f(x)=2sin($\frac{π}{4}$x+$\frac{π}{4}$),
故选:D.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
相关题目
19.已知P:0<x<2,Q:x(x-3)<0,¬P是¬Q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.已知数列{an}是等差数列,其a1=-8,a3=-4,Sn是数列{an}的前n项和,则( )
| A. | S8<S3 | B. | S8=S3 | C. | S6<S3 | D. | S6=S3 |
2.若集合A={x|-1≤x<2},B={x|x≥1},则A∩B=( )
| A. | (1,2) | B. | [-1,2】 | C. | [-1,1] | D. | [1,2) |
 已知A,B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1左、右顶点,过椭圆中心0作弦MN交椭圆于M,N两点,且$\overrightarrow{AN}$$•\overrightarrow{MN}$=0,|$\overrightarrow{MN}$|=2|$\overrightarrow{AN}$|.
已知A,B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1左、右顶点,过椭圆中心0作弦MN交椭圆于M,N两点,且$\overrightarrow{AN}$$•\overrightarrow{MN}$=0,|$\overrightarrow{MN}$|=2|$\overrightarrow{AN}$|.