题目内容
甲、乙两人约定傍晚6时到7时之间在某处会面,并约定先到者应等候另一人20分钟,过时即可离去,则两人在傍晚6时到7时之间会面的概率是 .
考点:几何概型
专题:概率与统计
分析:分析:由题意知本题是一个几何概型,试验发生包含的所有事件对应的集合是Ω={(x,y)|6≤x≤7,6≤y≤7}作出集合对应的面积是边长为1的正方形的面积,写出满足条件的事件对应的集合和面积,根据面积之比得到概率.
解答:
解:由题意知本题是一个几何概型,
∵试验发生包含的所有事件对应的集合是Ω={(x,y)|6≤x≤7,6≤y≤7},
集合对应的面积是边长为1的正方形的面积s=1,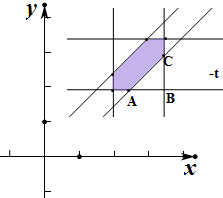
而满足条件的事件对应的集合是{(x,y)|6≤x≤7,6≤y≤7,|x-y|≤
},
对应的区域为阴影部分,其中A(
,6),B(7,6),C(7,
),
则△ABC的面积为
×
×
=
,
∴两人能够会面的概率是
=
故答案为:
.
∵试验发生包含的所有事件对应的集合是Ω={(x,y)|6≤x≤7,6≤y≤7},
集合对应的面积是边长为1的正方形的面积s=1,

而满足条件的事件对应的集合是{(x,y)|6≤x≤7,6≤y≤7,|x-y|≤
| 1 |
| 3 |
对应的区域为阴影部分,其中A(
| 19 |
| 3 |
| 20 |
| 3 |
则△ABC的面积为
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
∴两人能够会面的概率是
1-2×
| ||
| 1 |
| 5 |
| 9 |
故答案为:
| 5 |
| 9 |
点评:本题的难点是把时间分别用x,y坐标来表示,从而把时间长度这样的一维问题转化为平面图形的二维面积问题,转化成面积型的几何概型问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
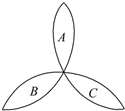 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
给出程序框图,若输入的x值为-5,则输出的y的值是( )


| A、-2 | B、-1 | C、0 | D、1 |
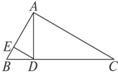 如图,在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,D、E为垂足,若AE=4,BE=1,则AC=
如图,在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,D、E为垂足,若AE=4,BE=1,则AC=