题目内容

已知a0=20.5，b=log32，c=log20.1，则（　　）
A、a＜b＜c
B、c＜a＜b
C、c＜b＜a
D、b＜c＜a
考点：对数值大小的比较
专题：函数的性质及应用
分析：利用指数函数和对数函数的单调性即可得出．
解答： 解：∵a=20.5＞20=1，0＜b=log32＜log33=1，c=log20.1＜log21=0．
∴c＜b＜a．
故选：C．
点评：本题考查了指数函数和对数函数的单调性，属于基础题．
练习册系列答案
相关题目
设变量x，y满足约束条件
y≤x+1
y≥2x-4
x+2y≥2
，则目标函数z=3x-2y的最大值为
 
．
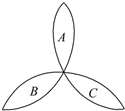荷花池中，有一只青蛙在成品字形的三片荷叶上跳来跳去（每次跳跃时，均从一叶跳到另一叶），而且逆时针方向跳的概率是顺时针方向跳的概率的两倍，如图所示．假设现在青蛙在A叶上，则跳四次之后停在A叶上的概率是（　　）
A、
4
9
B、
8
27
C、
16
81
D、
32
81
给出程序框图，若输入的x值为-5，则输出的y的值是（　　）
A、-2B、-1C、0D、1
已知向量
a
=（1，x），
b
=（x-1，2），若
a
∥
b
，则x=（　　）
A、-1或2B、-2或1
C、1或2D、-1或-2
双曲线C1的中心在原点，焦点在x轴上，若C1的一个焦点与抛物线C2：y2=12x的焦点重合，且抛物线C2的准线交双曲线C1所得的弦长为4
3
，则双曲线C1的实轴长为（　　）
A、6
B、2
6
C、
3
D、2
3
已知函数f（x）=
3
x
，则它在下列区间上不是减函数的是（　　）
A、（0，+∞）
B、（-∞，0）
C、（-∞，0）∪（0，+∞）
D、（1，+∞）
在平面直角坐标系xOy中，已知抛物线C：y2=4x，F为其焦点，点E的坐标为（2，0），设M为抛物线C上异于顶点的动点，直线MF交抛物线C于另一点N，链接ME，NE并延长分别交抛物线C与点P，Q．
（1）当MN⊥Ox时，求直线PQ与x轴的交点坐标；
（2）当直线MN，PQ的斜率存在且分别记为k1，k2时，求证：k1=2k2．
如图所示，边长为2的正方形中有一封闭曲线围成的阴影区域，在正方形中随机撒一粒豆子，若它落在阴影区域内的概率为
3
5
，则阴影区域的面积为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网