题目内容
2011年春,为保证全市居民用水,某市新建一个水库,已知该市在雨季的10天中,时间x(单位:天,1≤x≤10,x∈N*)和水库水位y(单位:米)的函数关系大致为y=-x2+12x+b,且在这10天中,水库的最低水位为3米.
(1)求b的值.
(2)若这10天水库没有决堤,则水库最低高多少米?
(1)求b的值.
(2)若这10天水库没有决堤,则水库最低高多少米?
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)由已知中函数的解析式,分析出函数的最小值,进而构造关于b的方程,解方程可得答案.
(2)由(1)中函数的解析式,结合二次函数的图象和性质,分析出函数的最大值,进而可得答案.
(2)由(1)中函数的解析式,结合二次函数的图象和性质,分析出函数的最大值,进而可得答案.
解答:
解:(1)∵时间x(单位:天,1≤x≤10,x∈N*)和水库水位y(单位:米)的函数关系大致为y=-x2+12x+b,
其图象是开口朝下,且以直线x=6为对称轴的抛物线,
故当x=1时,y取最小值,即b+11=3,
解得b=-8;
(2)由(1)可得y=-x2+12x-8
故当x=6时,y取最大值28,
即若这10天水库没有决堤,则水库最低高28米.
其图象是开口朝下,且以直线x=6为对称轴的抛物线,
故当x=1时,y取最小值,即b+11=3,
解得b=-8;
(2)由(1)可得y=-x2+12x-8
故当x=6时,y取最大值28,
即若这10天水库没有决堤,则水库最低高28米.
点评:本题主要考查了二次函数的函数的图象和性质,熟练二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
在△ABC中,BC=
,AC=3,sinC=2sinA,则tan(A-
)的值为( )
| 5 |
| π |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
| D、3 |
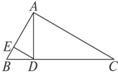 如图,在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,D、E为垂足,若AE=4,BE=1,则AC=
如图,在△ABC中,∠BAC=90°,AD⊥BC,DE⊥AE,D、E为垂足,若AE=4,BE=1,则AC=