题目内容
已知x，y满足约束条件
，则z=x+2y的最大值为（ ）
|
| A、-2 | B、-1 | C、1 | D、2 |
考点：简单线性规划
专题：不等式的解法及应用
分析：先画出满足条件的平面区域，将z=x+2y转化为：y=-
x+
，通过图象得出函数过（0，1）时，z取到最大值，求出即可．
| 1 |
| 2 |
| z |
| 2 |
解答：
解：画出满足条件的平面区域，
如图示：
，
将z=x+2y转化为：y=-
x+
，
通过图象得出函数过（0，1）时，z取到最大值，
zmax=2，
故选：D．
如图示：
，将z=x+2y转化为：y=-
| 1 |
| 2 |
| z |
| 2 |
通过图象得出函数过（0，1）时，z取到最大值，
zmax=2，
故选：D．
点评：本题考查了简单的线性规划问题，考查了数形结合思想，是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知命题p：若x＞y，则-x＜-y，q：?x0＞0，（x0+1）e x0≤1，下列命题为真的是（ ）
| A、p∧q |
| B、（￢p）∨q |
| C、（￢p）∨（￢q） |
| D、p∨（￢q） |
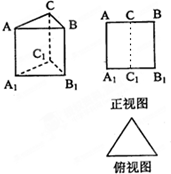如图，水平放置的三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥面A1B1C1，正视图是边长为2的正方形，俯视图为一个等边三角形，该三棱柱的左视图面积为（ ）