Question

已知三棱台ABC-A₁B₁C₁的上底面面积为a²，下底面面积为b²（a＞0，b＞0），作截面AB₁C₁，设三棱锥B-AB₁C₁的高等于三棱台的高，求△AB₁C₁的面积．

Answer 1

考点：棱台的结构特征

专题：空间位置关系与距离

分析：连接BC₁后，我们可以将三棱台ABC-A₁B₁C₁体积分为三个三棱锥的体积之和，根据已知中上底面ABC的面积为a²，下底面面积为b²（b＞a＞0），直线BC与平面AB₁C₁的距离等于这个三棱台的高，结合棱台和棱锥体积公式即可得到截面AB₁C₁的面积．

解答： 解：连接BC₁，如下图所示：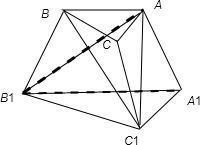
设三棱台的高为h，
则VABC-A1B1C1=

1

3

（S△ABC+

S△ABC•S△A1B1C1

+S△A1B1C1）h
=VA1-ABC+VA-A1B1C1+VB-AB1C1
=

1

3

S_△ABCh+

1

3

S△A1B1C1h+

1

3

S△AB1C1h，
∴

S△ABC•S△A1B1C1

=S△AB1C1，
又∵上底面ABC的面积为a²，下底面面积为b²
∴S△AB1C1=ab
所以△AB₁C₁的面积为ab．

点评：本题考查的知识点是棱台的体积公式和棱锥的体积公式，将棱台的体积VABC-A1B1C1分成三个三棱锥的体积和是解答本题的关键．