题目内容

三名射手独立地进行射击，甲中靶的概率是0.9，乙、丙中靶的概率均为0.8，三人中恰有两人中靶的概率（　　）
A、0.352B、0368
C、0.412D、0.214
考点：计数原理的应用
专题：概率与统计
分析：设甲，乙，丙中靶分别为事件A，B，C，则三人中恰有两人中靶为：（A∩B∩
.
C
）∪（A∩
.
B
∩C）∪（
.
A
∩B∩C），代入公式，可得答案．
解答： 解：设甲，乙，丙中靶分别为事件A，B，C，
则P（A）=0.9，P（B）=P（C）=0.8，
∴P（
.
A
）=0.1，P（
.
B
）=P（
.
C
）=0.2，
∵三人中恰有两人中靶为事件：（A∩B∩
.
C
）∪（A∩
.
B
∩C）∪（
.
A
∩B∩C），
故三人中恰有两人中靶的概率P=P（A∩B∩
.
C
）+P（A∩
.
B
∩C）+P（
.
A
∩B∩C）
=P（A）P（B）P（
.
C
）+P（A）P（
.
B
）P（C）+P（
.
A
）P（B）P（C），
=0.9×0.8×0.2+0.9×0.2×0.8+0.1×0.8×0.8
=0.352，
故选：A
点评：本题考查的知识点是相互独立事件概率乘法公式和互斥事件概率加法公式，其中分析出三人中恰有两人中靶为：（A∩B∩
.
C
）∪（A∩
.
B
∩C）∪（
.
A
∩B∩C），是解答的关键．
练习册系列答案
相关题目
设?的分布列为
? 1 2 3 4
P
1
6
1
6
1
3
1
3
又设y=2?+5 则 Ey=（　　）
A、
7
6
B、
17
6
C、
17
3
D、
32
3
设正项等比数列{an}的前n项和为Sn，且210S30+S10=（210+1）S20，则数列{an}的公比为（　　）
A、1
B、
1
2
C、
1
4
D、
1
8
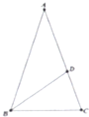学习“三角”时，小明同学在参考书上看到求sin18°精确值的一种方法，具体如下：设等腰△ABC的顶角∠A=36°．底角∠B的平分线交腰AC于D，且BC=1（如图），则AD=BD=1，于是，在△BCD中，可得CD=2sin18°．由△BAC∽△CBD得
AC
BC
=
BD
CD
，即
1+2sin18°
1
=
1
2sin18°
，整理得4sin218°+2sin18°-1=0，又sin18°（0，1），故解得sin18°=
5
-1
4
．现设α，β，α+β均属于区间（0，
π
2
），若cos（
3π
2
-2β）•sin（2α+β）=cos（
π
2
+2α）•sin（α+2β），则下列命题正确的是（　　）
A、关于x的方程α•4x+β•2x+α=0有实数解
B、关于x的方程α•（log4x）2+β•log4x-α=0无实数解
C、关于x的方程sinx=
2β-α
α
有实数解
D、关于x的方程cosx=
β
2a+β
无实数解
已知定义域为R的函数f（x）满足：f（x+π）=
f(x)
π
，且x∈[-
π
2
，
π
2
]时，f（x）=xsinx+cosx-
π
2
，则当x∈[-3π，-2π]时，f（x）的最小值为（　　）
A、
2π3-π4
2
B、
2π2-π3
2
C、
2-π
2π
D、
2-π
2π2
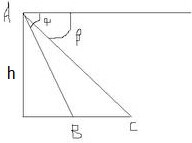如图，从高为h的气球（A）上测量铁桥（BC）的长，如果测得桥头B的俯角是α，桥头C的俯角是β，则该桥的长可表示为（　　）
A、
sin(α-β)
sinαsinβ
•h
B、
sin(α-β)
cosαsinβ
•h
C、
sin(α-β)
cosαcosβ
•h
D、
cos(α-β)
cosαcosβ
•h
已知函数f（x）=sinx-x，则下列错误的是（　　）
A、f（x）为奇函数
B、f（x）在R上单调递减
C、f（x）在R上无极值点
D、f（x）在R上有三个零点
一盒中装有5个产品，其中有3个一等品，2个二等品，从中不放回地取出产品，每次1个，取两次，已知第二次取得一等品的条件下，第一次取得的是二等品的概率是（　　）
A、
1
2
B、
1
3
C、
1
4
D、
2
3
（1）化简：
tan(π-α)•sin(
π
2
+α)•cos(2π-α)
cos(-π-α)•tan(α-2π)

（2）设
a
=（1，0），
b
=（1，1），若向量λ
a
+
b
与向量
c
=（6，2）共线，求实数λ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网