题目内容
16．
如图，AB是圆O的直径，P是圆弧AB上的点，M、N是AB上的两个三等分点，且AB=6，则$\overrightarrow{PM}•\overrightarrow{PN}$=8．
分析 $\overrightarrow{PM}$=$\overrightarrow{PO}$+$\overrightarrow{OM}$，$\overrightarrow{PN}$=$\overrightarrow{PO}+\overrightarrow{ON}$，$|\overrightarrow{PO}|$=3，$\overrightarrow{OM}+\overrightarrow{ON}$=$\overrightarrow{0}$，$\overrightarrow{OM}$=$\frac{1}{2}\overrightarrow{MN}$=$\frac{1}{6}$$\overrightarrow{AB}$=-$\overrightarrow{ON}$．代入计算即可得出．
解答 解：∵$\overrightarrow{PM}$=$\overrightarrow{PO}$+$\overrightarrow{OM}$，$\overrightarrow{PN}$=$\overrightarrow{PO}+\overrightarrow{ON}$，$|\overrightarrow{PO}|$=3，$\overrightarrow{OM}+\overrightarrow{ON}$=$\overrightarrow{0}$，$\overrightarrow{OM}$=$\frac{1}{2}\overrightarrow{MN}$=$\frac{1}{6}$$\overrightarrow{AB}$=-$\overrightarrow{ON}$．
∴$\overrightarrow{PM}•\overrightarrow{PN}$=（$\overrightarrow{PO}$+$\overrightarrow{OM}$）•（$\overrightarrow{PO}+\overrightarrow{ON}$）=${\overrightarrow{PO}}^{2}$+$\overrightarrow{PO}$•$（\overrightarrow{OM}+\overrightarrow{ON}）$+$\overrightarrow{OM}•\overrightarrow{ON}$
=32-$\frac{1}{36}×{6}^{2}$
=8，
故答案为：8．
点评 本题考查了向量的三角形法则、数量积运算性质、向量共线定理，考查了推理能力与计算能力，属于中档题．
| A． | $\frac{2ab}{a+b}$＜$\frac{a+b}{2}$＜$\sqrt{ab}$ | B． | $\sqrt{ab}$≤$\frac{2ab}{a+b}$≤$\frac{a+b}{2}$ | C． | $\frac{2ab}{a+b}$＜$\sqrt{ab}$＜$\frac{a+b}{2}$ | D． | $\sqrt{ab}$＜$\frac{2ab}{a+b}$＜$\frac{a+b}{2}$ |
| A． | 3x-y+1=0 | B． | 3x+y-5=0 | C． | 3x-y-5=0 | D． | 3x+y-1=0 |
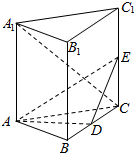已知三棱柱ABC-A1B1C1，侧棱AA1垂直于底面ABC，∠ABC=$\frac{π}{2}$，AB=BC=AA1=4，D为BC的中点．
如图，有一块矩形空地，要在这块空地上开辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB=a（a＞2），BC=2，且AE=AH=CF=CG，设AE=x，绿地面积为y．| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $±\frac{1}{2}$ | D． | $±\frac{{\sqrt{3}}}{2}$ |