题目内容
若a1=12，a2=12+22+12，…，an=12+22+…+n2+…+22+12，在运用数学归纳法证明an=
n（2n2+1）时，第二步中从k到k+1应添加的项是（ ）
| 1 |
| 3 |
| A、k2+1 |
| B、（k2+1）2 |
| C、（k+1）2+k2 |
| D、（k+1）2+2k2 |
考点：数学归纳法
专题：计算题,点列、递归数列与数学归纳法
分析：ak=12+22+…+k2+…+22+12，ak+1=12+22+…+k2+（k+1）2+k2+…+22+12，即可得出结论．
解答：
解：∵ak=12+22+…+k2+…+22+12，ak+1=12+22+…+k2+（k+1）2+k2+…+22+12，
∴在运用数学归纳法证明an=
n（2n2+1）时，第二步中从k到k+1应添加的项是（k+1）2+k2，
故选：C．
∴在运用数学归纳法证明an=
| 1 |
| 3 |
故选：C．
点评：本题考查数学归纳法的运用，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
不等式x2≥2x的解集是（ ）
| A、{x|x≥2} |
| B、{x|x≤2} |
| C、{x|0≤x≤2} |
| D、{x|x≤0或x≥2} |
如图所示，程序框图（算法流程图）的输出结果是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1（a＞0，b＞0）左、右焦点分别为F1（-c，0），F2（c，0），若双曲线右支上存在点P使得
=
，则该双曲线离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| sin∠PF1F2 |
| c |
| sin∠PF2F1 |
A、（0，
| ||
B、（
| ||
C、（1，
| ||
D、（
|
已知数列{an}满足an+1=2an-an-1（n≥2），且a1=1，a2=2，则数列{
}的前10项之和等于（ ）
| 1 |
| anan+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f（x）=x3-4，则零点一定在（ ）
| A、（1，2） |
| B、（2，3） |
| C、（3，4） |
| D、（5，6） |
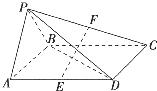四棱锥P-ABCD的底面是平行四边形，平面PAB⊥平面ABCD，PA=PB=AB=