题目内容
9．若关于x，y的方程组$\left\{{\begin{array}{l}{ax+y-1=0}\\{4x+ay-2=0}\end{array}}\right.$有无数多组解，则实数a=2．分析 根据题意，若关于x，y的方程组有无数多组解，则直线ax+y-1=0与直线4x+ay-2=0重合，分析可得$\frac{a}{4}$=$\frac{1}{a}$=$\frac{-1}{-2}$，解可得a的值，即可得答案．
解答 解：根据题意，若关于x，y的方程组$\left\{{\begin{array}{l}{ax+y-1=0}\\{4x+ay-2=0}\end{array}}\right.$有无数多组解，
则直线ax+y-1=0与直线4x+ay-2=0重合，
则有$\frac{a}{4}$=$\frac{1}{a}$=$\frac{-1}{-2}$，
解可得a=2，
故答案为：2．
点评 本题考查直线的一般式方程，涉及直线的方程与直线的关系，注意关于x、y的二元一次方程组有无数多组解等价于两直线重合．
练习册系列答案
相关题目
19．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的右焦点为F2，O为坐标原点，M为y轴上一点，点A是直线MF2与椭圆C的一个交点，且|OA|=|OF2|=2|OM|，则椭圆C的离心率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{5}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{\sqrt{5}}{3}$ |
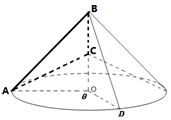如图，等腰Rt△AOB，OA=OB=2，点C是OB的中点，△AOB绕BO所在的边逆时针旋转一周．