题目内容
设α是第二象限角，则
是（ ）
| α |
| 2 |
| A、第一象限角 |
| B、第一或第三象限角 |
| C、第二象限角 |
| D、第一或第二象限角 |
考点：象限角、轴线角
专题：三角函数的求值
分析：由α的范围判断θ的一半的范围，先写出角的范围，再除以2，求出角的一半的范围，看出角的范围．
解答：
解：∵α是第二象限角，
∴α∈（2kπ+
，2kπ+π）
∴
∈（kπ+
，kπ+
）
∴
是第一或三象限角，
故选：B．
∴α∈（2kπ+
| π |
| 2 |
∴
| α |
| 2 |
| π |
| 4 |
| π |
| 2 |
∴
| α |
| 2 |
故选：B．
点评：本题考查了角的范围，考查象限角，本题解题的关键是写出象限角的范围，根据不等式的做法，写出要求的角的范围．
练习册系列答案
优学名师名题系列答案
相关题目
已知向量
=（1，2），
=（x，-4），若
与
共线，则x的值为（ ）
| a |
| b |
| a |
| b |
| A、2 | B、8 | C、±2 | D、-2 |
有三个球，一个球内切于正方体的各个面，另一个球切正方体的各条棱，第三个球过正方体的各个顶点（都是同一正方体），则这三个球的体积之比为（ ）
A、1：
| ||||
| B、1：2：3 | ||||
C、1：2
| ||||
| D、1：4：3 |
现有四件不同款式的上衣与三件不同颜色的长裤，如果一条长裤与一件上衣配成一套，则不同的选法数为（ ）
| A、7 | B、64 | C、12 | D、81 |
从10名班委中选出两名担任班长和副班长；有（ ）种不同选法．
A、
| ||
B、
| ||
C、
| ||
| D、2 |
函数y=
的定义域为（ ）
| 1 | ||
|
| A、（-4，-1） |
| B、（-4，1） |
| C、（-1，1） |
| D、（-1，1] |
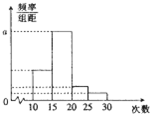对某校高一年级学生参加社区服务次数统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：