题目内容
数列
,-
,
,-
,…的一个通项公式是 .
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
考点:数列的函数特性
专题:等差数列与等比数列
分析:由数列
,-
,
,-
,…可知:第n项的符号为(-1)n+1,其绝对值为
.即可得出此数列的一个通项公式.
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| n |
| n+1 |
解答:
解:由数列
,-
,
,-
,…可知:第n项的符号为(-1)n+1,其绝对值为
.
可得此数列的一个通项公式是:an=(-1)n+1•
.
故答案为:an=(-1)n+1•
.
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| n |
| n+1 |
可得此数列的一个通项公式是:an=(-1)n+1•
| n |
| n+1 |
故答案为:an=(-1)n+1•
| n |
| n+1 |
点评:本题考查了通过观察、方向、猜想、归纳法球数列的通项公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
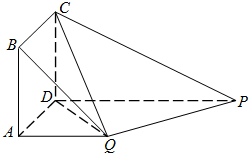 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ= 如图,O、A、B是平面上的三点,P为线段AB的中垂线上的任意一点,若|
如图,O、A、B是平面上的三点,P为线段AB的中垂线上的任意一点,若| 如图,在矩形OABC中,点E,F分别在AB,BC上,且满足AB=3AE,BC=3CF,若
如图,在矩形OABC中,点E,F分别在AB,BC上,且满足AB=3AE,BC=3CF,若