题目内容
17.若(3x-1)5=a0+a1x+a2x2+…+a5x5,则a1+2a2x+3a3x+4a4+5a5=( )| A. | 80 | B. | 120 | C. | 180 | D. | 240 |
分析 对已知等式求导数,对求导后的等式中的x赋值1,求出a1+2a2+3a3+4a4+5a5的值.
解答 解:∵(3x-1)5=a0+a1x+a2x2+…+a5x5,
两边求导可得:15(3x-1)4=a1+2a2x+…+5a5x4,
令x=1,可得a1+2a2x+3a3x+4a4+5a5=15(3-1)4=240,
故选:D.
点评 本题考查复合函数的求导法则、考查赋值法求展开式的系数和常用的方法.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
12.若变量x,y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ 2x-y-1≤0\\ x+y+1≥0\end{array}\right.$,则目标函数z=2x+y的最小值为( )
| A. | 4 | B. | -1 | C. | -2 | D. | -3 |
2.设{an}是公比负数的等比数列,a1=2,a3-4=a2,则a3=( )
| A. | 2 | B. | -2 | C. | 8 | D. | -8 |
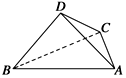 如图所示,四面体ABCD中,已知平面BCD⊥平面ABC,BD⊥DC,BC=6,AB=4$\sqrt{3}$,∠ABC=30°.
如图所示,四面体ABCD中,已知平面BCD⊥平面ABC,BD⊥DC,BC=6,AB=4$\sqrt{3}$,∠ABC=30°. 已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.则在本次数学竞赛中,成绩在[80,90]上的学生人数为900.
已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.则在本次数学竞赛中,成绩在[80,90]上的学生人数为900.