题目内容
1.若x,y满足约束条件$\left\{{\begin{array}{l}{x+y-2≤0}\\{x-2y+1≤0}\\{2x-y+2≥0}\end{array}}\right.$,则Z=x2+y2的最小值为2.分析 作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
解答 解:作出x,y满足约束条件$\left\{{\begin{array}{l}{x+y-2≤0}\\{x-2y+1≤0}\\{2x-y+2≥0}\end{array}}\right.$,对应的平面区域如图,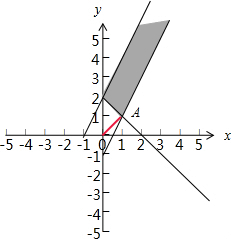
z的几何意义为区域内的点到原点的距离的平方,
由图象知:
OA的距离最小,
由$\left\{\begin{array}{l}{x+y=2}\\{x-2y+1=0}\end{array}\right.$,解得A(1,1),
则|OA|2=12+12=2,
故z的最小值为d2=2,
故答案为:2.
点评 本题主要考查线性规划的应用以及两点间的距离公式的应用,利用数形结合是解决本题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
17.若(3x-1)5=a0+a1x+a2x2+…+a5x5,则a1+2a2x+3a3x+4a4+5a5=( )
| A. | 80 | B. | 120 | C. | 180 | D. | 240 |
12.下列函数中,与函数y=-3|x|的奇偶性相同,且在(-∞,0)上单调性也相同的是( )
| A. | y=1-x2 | B. | y=log2|x| | C. | y=-$\frac{1}{x}$ | D. | y=x3-1 |
9.“x>3”是“$\frac{1}{x}$$<\frac{1}{3}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
6.若角θ满足$cosθ+sinθ=\frac{1}{2}$,则角θ是( )
| A. | 第一项限角或第二象限角 | B. | 第二象限角或第四象限角 | ||
| C. | 第一象限角或第三象限角 | D. | 第二象限角或第三象限角 |
13.已知集合A={x|y=$\sqrt{x}$},B={x|x2+x>0},则A∩B=( )
| A. | {x|x>0} | B. | {x|x≥0} | C. | {x|0<x<1} | D. | {x|x<1} |
10.若f(x)=2xf'(1)+x2,则f'(0)=( )
| A. | $\frac{1}{2}$ | B. | 6 | C. | -2 | D. | -4 |
11.已知数列{an}为等差数列,若a8=4,则数列{an}的前15项和S15=( )
| A. | 12 | B. | 32 | C. | 60 | D. | 120 |