题目内容
3.(Ⅰ)化简$\frac{cos(α-\frac{3}{2}π)}{sin(\frac{π}{2}+α)}$•sin(α-π)•cos(2π-α);(Ⅱ)已知sin θ=$\frac{12}{13}$,θ为锐角,求cos($\frac{π}{4}$-θ).
分析 (Ⅰ)利用诱导公式化简即可;
(Ⅱ)根据平方公式求出cosθ的值,再利用两角差的余弦公式求值即可.
解答 解:(Ⅰ)$\frac{cos(α-\frac{3}{2}π)}{sin(\frac{π}{2}+α)}$•sin(α-π)•cos(2π-α)
=$\frac{-sinα}{cosα}$•(-sinα)•cosα
=sin2α;
(Ⅱ)sin θ=$\frac{12}{13}$,θ为锐角,
∴cosθ=$\sqrt{1{-sin}^{2}θ}$=$\frac{5}{13}$
∴cos($\frac{π}{4}$-θ)=cos$\frac{π}{4}$cosθ+sin$\frac{π}{4}$sinθ
=$\frac{\sqrt{2}}{2}$×$\frac{5}{13}$+$\frac{\sqrt{2}}{2}$×$\frac{12}{13}$
=$\frac{17\sqrt{2}}{26}$.
点评 本题考查了三角函数诱导公式与求值计算问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知数列2008,2009,1,-2008,…若这个数列从第二项起,每一项都等于它的前后两项之和,则这个数列的前2017项之和S2017等于( )
| A. | 0 | B. | 2008 | C. | 2017 | D. | 4017 |
18.平面 α∥平面 β,直线 a⊆α,下列四个说法中,正确的个数是
①a与β内的所有直线平行;
②a与β内的无数条直线平行;
③a与β内的任何一条直线都不垂直;
④a与β无公共点.( )
①a与β内的所有直线平行;
②a与β内的无数条直线平行;
③a与β内的任何一条直线都不垂直;
④a与β无公共点.( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
15.函数f(x)=x3+ax2+(a-3)x(a∈R)的导函数是f'(x),若f'(x)是偶函数,则以下结论正确的是( )
| A. | y=f(x)的图象关于y轴对称 | B. | y=f(x)的极小值为-2 | ||
| C. | y=f(x)的极大值为-2 | D. | y=f(x)在(0,2)上是增函数 |
13.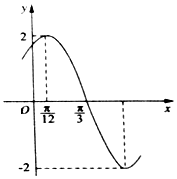 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )| A. | 函数f(x)的图象关于直线x=-$\frac{2π}{3}$对称 | |
| B. | 函数f(x)的图象关于点(-$\frac{11π}{12}$,0)对称 | |
| C. | 若方程f(x)=m在[-$\frac{π}{2}$,0]上有两个不相等的实数根,则实数m∈(-2,-$\sqrt{3}$] | |
| D. | 将函数f(x)的图象向左平移$\frac{π}{6}$个单位可得到一个偶函数 |