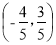题目内容
20．若f（x）=$\frac{1}{{{2^x}+2}}$+a是奇函数，则a=-$\frac{1}{3}$．分析 由题意，f（0）=$\frac{1}{3}+a$=0，即可得出结论．
解答 解：由题意，f（0）=$\frac{1}{3}+a$=0，∴a=$-\frac{1}{3}$．
故答案为-$\frac{1}{3}$．
点评 本题考查奇函数的性质，考查学生的计算能力，比较基础．
练习册系列答案
智慧小复习系列答案
相关题目
11．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是120°，且|$\overrightarrow{a}$|=5，|$\overrightarrow{b}$|=4，则$\overrightarrow{a}$•$\overrightarrow{b}$=（ ）
| A． | 20 | B． | 10 | C． | -10 | D． | -20 |
12．
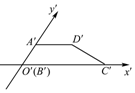已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′（如图所示），其中A′D′=2，B′C′=4，A′B′=1，则直角梯形DC边的长度是（ ）
已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′（如图所示），其中A′D′=2，B′C′=4，A′B′=1，则直角梯形DC边的长度是（ ）| A． | $\sqrt{5}$ | B． | $2\sqrt{2}$ | C． | $2\sqrt{5}$ | D． | $\sqrt{3}$ |
9．“0＜a＜1”是“a＜$\sqrt{a}$”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
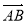同方向的单位向量为（ ）
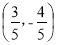B．
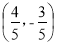
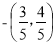D．