题目内容
10．命题“若m2+n2=0，则mn=0”的逆否命题是“若mn≠0，则m2+n2≠0”．分析 根据命题“若p，则q”的逆否命题是“若￢q，则￢p”，写出对应的命题即可．
解答 解：命题“若m2+n2=0，则mn=0”的逆否命题是
“若mn≠0，则m2+n2≠0”．
故答案为：“若mn≠0，则m2+n2≠0”．
点评 本题考查了命题和它的逆否命题的应用问题，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
20．函数y=cos（ωx+$\frac{π}{4}$）+1（ω＞0）的图象向右平移$\frac{2}{3}$π个单位后与原图象重合，则ω的最小值是（ ）
| A． | 6 | B． | 3 | C． | $\frac{3}{2}$ | D． | $\frac{2}{3}$ |
1．若点P的极坐标为（2$\sqrt{3}$，$\frac{2π}{3}$），则点P的直角坐标为（ ）
| A． | （-$\sqrt{3}$，3） | B． | （-3，$\sqrt{3}$） | C． | （3，-$\sqrt{3}$） | D． | （$\sqrt{3}$，-3） |
18．已知{an}是等比数列，{bn}是等差数列，若a2•a14=4a8，b8=a8，则数列{bn}的前15项和等于（ ）
| A． | 30 | B． | 40 | C． | 60 | D． | 120 |
5．
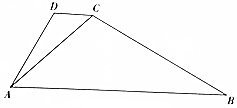如图，在梯形ABCD中，AB∥CD，∠DAC=30°，∠CAB=45°，CD=$\sqrt{6}$-$\sqrt{2}$．
（Ⅰ）求AD的长；
（Ⅱ）若BC=$\sqrt{10}$，求△ABC的面积．
如图，在梯形ABCD中，AB∥CD，∠DAC=30°，∠CAB=45°，CD=$\sqrt{6}$-$\sqrt{2}$．（Ⅰ）求AD的长；
（Ⅱ）若BC=$\sqrt{10}$，求△ABC的面积．
15．如果直线l上的一点A沿x轴在正方向平移1个单位，再沿y轴负方向平移3个单位后，又回到直线l上，则l的斜率是（ ）
| A． | 3 | B． | $\frac{1}{3}$ | C． | -3 | D． | $-\frac{1}{3}$ |
2．$sin\frac{5π}{3}$=（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |