题目内容
11．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是120°，且|$\overrightarrow{a}$|=5，|$\overrightarrow{b}$|=4，则$\overrightarrow{a}$•$\overrightarrow{b}$=（ ）| A． | 20 | B． | 10 | C． | -10 | D． | -20 |
分析 利用数量积公式解答即可．
解答 解：向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是120°，且|$\overrightarrow{a}$|=5，|$\overrightarrow{b}$|=4，则$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|×|$\overrightarrow{b}$|cos120°=5×4×（-$\frac{1}{2}$）=-10；
故选：C．
点评 本题考查了平面向量的数量积公式；属于基础题．
练习册系列答案
相关题目
1．若点P的极坐标为（2$\sqrt{3}$，$\frac{2π}{3}$），则点P的直角坐标为（ ）
| A． | （-$\sqrt{3}$，3） | B． | （-3，$\sqrt{3}$） | C． | （3，-$\sqrt{3}$） | D． | （$\sqrt{3}$，-3） |
2．$sin\frac{5π}{3}$=（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
16．已知函数$y=sin（ωx+φ）（ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示，则（ ）
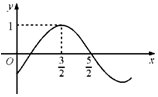
| A． | $ω=\frac{π}{2}，φ=-\frac{π}{4}$ | B． | ω=$\frac{π}{2}，φ=\frac{π}{4}$ | C． | $ω=π，φ=-\frac{π}{4}$ | D． | $ω=π，φ=\frac{π}{4}$ |
解集为 。