题目内容
12.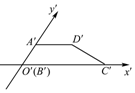 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{3}$ |
分析 由已知直角梯形ABCD中,AB⊥BC,AD=A′D′=2,BC=B′C′=4,AB=2A′B′=2,由此能求出直角梯形DC边的长度.
解答  解:由已知作出梯形ABCD是直角梯形,如右图:
解:由已知作出梯形ABCD是直角梯形,如右图:
∵按照斜二测画法画出它的直观图A′B′C′D′,A′D′=2,B′C′=4,A′B′=1,
∴直角梯形ABCD中,AB⊥BC,AD=A′D′=2,BC=B′C′=4,AB=2A′B′=2,
过D作DE⊥BC,交BC于E,则DE=AB=2,EC=BC-AD=4-2=2,
∴直角梯形DC边的长度为:$\sqrt{4+4}$=2$\sqrt{2}$.
故选:B.
点评 本题考查直角梯形中斜边长的求法,是基础题,解题时要认真审题,注意斜二测画法的合理运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
2.$sin\frac{5π}{3}$=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
 解集为 。
解集为 。 ,则△ABC的外心一定在满足条件的P点集合中;
,则△ABC的外心一定在满足条件的P点集合中; ,则△ABC的内心一定在满足条件的P点集合中;
,则△ABC的内心一定在满足条件的P点集合中; ,则△ABC的重心一定在满足条件的P点集合中;
,则△ABC的重心一定在满足条件的P点集合中; ,则△ABC的垂心一定在满足条件的P点集合中.
,则△ABC的垂心一定在满足条件的P点集合中. ,则△ABC的外心一定在满足条件的P点集合中.
,则△ABC的外心一定在满足条件的P点集合中.