题目内容
15．已知函数f（x）=$\left\{\begin{array}{l}\frac{1}{x^2}，x＜1\\{log_2}（{x+4}），x≥1\end{array}$，则$f（f（\frac{1}{2}））$=（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 8 |
分析 先求出f（$\frac{1}{2}$）=$\frac{1}{（\frac{1}{2}）^{2}}$=4，从而$f（f（\frac{1}{2}））$=f（4），由此能求出结果．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}\frac{1}{x^2}，x＜1\\{log_2}（{x+4}），x≥1\end{array}$，
∴f（$\frac{1}{2}$）=$\frac{1}{（\frac{1}{2}）^{2}}$=4，
$f（f（\frac{1}{2}））$=f（4）=log28=3．
故选：B．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
5．
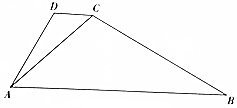如图，在梯形ABCD中，AB∥CD，∠DAC=30°，∠CAB=45°，CD=$\sqrt{6}$-$\sqrt{2}$．
（Ⅰ）求AD的长；
（Ⅱ）若BC=$\sqrt{10}$，求△ABC的面积．
如图，在梯形ABCD中，AB∥CD，∠DAC=30°，∠CAB=45°，CD=$\sqrt{6}$-$\sqrt{2}$．（Ⅰ）求AD的长；
（Ⅱ）若BC=$\sqrt{10}$，求△ABC的面积．
10．已知抛物线的参数方程为$\left\{{\begin{array}{l}{x=4{t^2}}\\{y=4t}\end{array}}\right.$，若斜率为1的直线经过抛物线的焦点，且与抛物线相交于A，B两点，则线段AB的长为（ ）
| A． | $2\sqrt{2}$ | B． | $4\sqrt{2}$ | C． | 8 | D． | 4 |
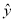＝2．347x－6．423；②y与x负相关且
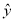＝－3．476x＋5．648；③y与x正相关且