题目内容
1．经过两圆x2+y2=9和（x+4）2+（y+3）2=8的交点的直线方程为（ ）| A． | 8x+6y+13=0 | B． | 6x-8y+13=0 | C． | 4x+3y+13=0 | D． | 3x+4y+26=0 |
分析 利用圆系方程，求解即可．
解答 解：联立x2+y2=9和（x+4）2+（y+3）2=8，作差可得：8x+6y+26=0，即6x-8y+13=0．
故选：B．
点评 本题考查圆系方程的应用，考查计算能力．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
12．
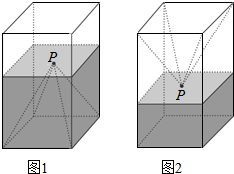如图1，一个正四棱柱形的密闭容器水平放置，其底部镶嵌了同底的正四棱锥形实心装饰块，容器内盛有a升水时，水面恰好经过正四棱锥的顶点P．如果将容器倒置，水面也恰好过点P（图2）．有下列四个结论，其中错误的代号是（ ）
如图1，一个正四棱柱形的密闭容器水平放置，其底部镶嵌了同底的正四棱锥形实心装饰块，容器内盛有a升水时，水面恰好经过正四棱锥的顶点P．如果将容器倒置，水面也恰好过点P（图2）．有下列四个结论，其中错误的代号是（ ）| A． | 若往容器内再注入a升水，则容器恰好能装满 | |
| B． | 将容器侧面水平放置时，水面也恰好过点P | |
| C． | 任意摆放该容器，当水面静止时，水面都恰好经过点P | |
| D． | 正四棱锥的高等于正四棱柱高的一半 |
9．与圆O1：x2+y2=1和圆O2：x2+y2-6x-8y+9=0都相切的直线条数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
16．若双曲线9y2-mx2=1的一个顶点到它的一条渐近线的距离为$\frac{1}{5}$，则m等于（ ）
| A． | 25 | B． | 16 | C． | 4 | D． | 1 |
10．“x≥0”是“log${\;}_{\frac{1}{2}}$（x+2）＜2”的（ ）
| A． | 充要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 既不充分也不必要条件 |
11．下列关于四个数：${e^{-\sqrt{2}}}，{log_{0.2}}3，lnπ，{（{a^2}+3）^0}（a∈R）$的大小的结论，正确的是（ ）
| A． | ${log_{0.2}}3＜{e^{-\sqrt{2}}}＜{（{a^2}+3）^0}＜lnπ$ | B． | ${e^{-\sqrt{2}}}＜{log_{0.2}}3＜{（{a^2}+3）^0}＜lnπ$ | ||
| C． | ${e^{-\sqrt{2}}}＜{（{a^2}+3）^0}＜{log_{0.2}}3＜lnπ$ | D． | ${log_{0.2}}3＜{（{a^2}+3）^0}＜{e^{-\sqrt{2}}}＜lnπ$ |