题目内容
16.已知实数a,b,c满足3a-b-c=0,则原点O(0,0)到直线ax+by+c=0的距离的最大值为$\sqrt{10}$.分析 根据直线方程和3a-b-c=0,得直线过定点(-3,1),所以原点O(0,0)到直线ax+by+c=0的距离的最大值即为原点到定点的距离.
解答 解:∵实数a,b,c满足3a-b-c=0,直线ax+by+c=0,
∴(-3)a+b+c=0.
∴直线过定点(-3,1),
∴原点O(0,0)到直线ax+by+c=0的距离的最大值即为原点(0,0)到定点(-3,1)的距离:
∵原点O(0,0)到定点(-3$\sqrt{(-3)^{2}+1}$=$\sqrt{10}$,
∴原点O(0,0)到直线ax+by+c=0的距离的最大值为$\sqrt{10}$.
故答案为:$\sqrt{10}$.
点评 本题考查点到直线的距离的最大值的求法,是基础题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
7.函数f(x)=-$\frac{1}{2}{x^3}$-sinx-2x的定义域为R,数列{an}是公差为d的等差数列,且a1+a2+a3+a4+…+a2015<0,记m=f(a1)+f(a2)+f(a3)+…+f(a2015),关于实数m,下列说法正确的是( )
| A. | m恒为负数 | |
| B. | 当d>0时,m恒为正数;当d<0时,m恒为负数 | |
| C. | m恒为正数 | |
| D. | 当d>0时,m恒为负数;当d<0时,m恒为正数 |
8.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
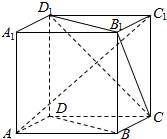

| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 异面直线AD与CB1角为60° | D. | AC1⊥平面CB1D1 |
 与圆
与圆 交于
交于 ,则
,则 的最小值为 .
的最小值为 .