题目内容
非空数集A={a1,a2,a3,…,an}(n∈N*,an)中,所有元素的算术平均数记为E(A),即E(A)=
.若非空数集B满足下列两个条件:
①B⊆A;
②E(B)=E(A),则称B为A的一个“保均值子集”.
据此,集合{1,2,3,4,5}的“保均值子集”的概率是( )
| a1+a2+a3+…+an |
| n |
①B⊆A;
②E(B)=E(A),则称B为A的一个“保均值子集”.
据此,集合{1,2,3,4,5}的“保均值子集”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:子集与真子集
专题:新定义,集合
分析:根据集合A和“保均值子集”的定义把集合的非空真子集列举出来,即可得到个数.
解答:
解:解:集合{1,2,3,4,5}的所有的子集个数有25=32,
∵非空数集A={1,2,3,4,5}中,所有元素的算术平均数E(A)=
=3,
∴集合A的“保均值子集”有:{3},{1,5},{2,4},{3,1,5},{3,2,4},{1,5,2,4},{1,2,3,4,5}共7个;
∴集合{1,2,3,4,5}的“保均值子集”的概率是
故选,A.
∵非空数集A={1,2,3,4,5}中,所有元素的算术平均数E(A)=
| 1+2+3+4+5 |
| 5 |
∴集合A的“保均值子集”有:{3},{1,5},{2,4},{3,1,5},{3,2,4},{1,5,2,4},{1,2,3,4,5}共7个;
∴集合{1,2,3,4,5}的“保均值子集”的概率是
| 7 |
| 32 |
故选,A.
点评:本题考查的知识点是计算集合子集的个数,众数、中位数、平均数,属于基础题

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
函数y=Asin(ωx+φ)+k(A>0,ω>0,|φ|≤
,x∈R)的部分图象如图所示,则该函数表达式为( )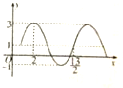
| π |
| 6 |

A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(
| ||||
D、y=2sin(
|
函数y=
的定义域为( )
| 1-lnx |
| A、(0,e] |
| B、(-∞,e] |
| C、(0,10] |
| D、(-∞,10] |
函数y=
的定义域为( )
| ||
| lg(2x-2) |
| A、[1,2] | ||||
| B、(1,2] | ||||
C、(1,
| ||||
D、[1,
|
已知正方体ABCD-A1B1C1D1中,平面BDC1∩平面A1B1C1D1=l,则直线BD与交线l的位置关系是( )
| A、平行 | B、相交 |
| C、异面 | D、平行或异面 |
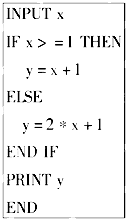 读程序,完成下列题目:程序如图:
读程序,完成下列题目:程序如图: