题目内容

函数y=
2x2+5x+7
x+1
（x＞-1）的最小值为
 
．
考点：基本不等式在最值问题中的应用
专题：不等式的解法及应用
分析：化简函数的解析式，然后利用基本不等式求解最小值即可．
解答： 解：函数y=
2x2+5x+7
x+1
=2（x+1）+
4
x+1
+1，
∵x＞-1，∴x+1＞0，
y=2（x+1）+
4
x+1
+1≥2
2(x+1)•
4
x+1
+1=4
2
+1，
当且仅当x+1=
2
x+1
即x=
2
-1时等号成立．
函数的最小值为：4
2
+1．
故答案为：4
2
+1．
点评：本题考查基本不等式求解函数的最值，基本知识的考查．
练习册系列答案
相关题目
集合{1，2，3}的真子集的个数有（　　）
A、8个B、7个
C、6 个D、5个
非空数集A={a1，a2，a3，…，an}（n∈N*，an）中，所有元素的算术平均数记为E（A），即E（A）=
a1+a2+a3+…+an
n
．若非空数集B满足下列两个条件：
①B⊆A；
②E（B）=E（A），则称B为A的一个“保均值子集”．
据此，集合{1，2，3，4，5}的“保均值子集”的概率是（　　）
A、
7
32
B、
3
16
C、
5
32
D、
1
8
复数
3-i
1-i
的虚部=
 
．
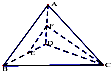如图，在三棱锥A-BCD中，BC=CD=DB，AB=AC=AD；E，F为棱BD，AD的中点，若EF⊥CF，则直线BD与平面ACD所成的角为
 
．
设集合A={x|log 
1
2
（3-x）≥-2}，B={x|
2a
x-a
＞1}．
（1）求集合B；
（2）若A∩B≠∅，求实数a的取值范围．
对于下列命题：
①命题“?x0∈R，x02+1＞3x0”的否定是“?x∈R，x2+1≤3x”；
②在△ABC中“∠A＞∠B”的 充要条件是“sinA＞sinB”；
③设a=sin
2014π
3
，b=cos
2014π
3
，c=tan
2014π
3
，则c＞a＞b；
④将函数y=2sin（3x+
π
6
）图象的横坐标变为原来的3倍，再向左平移
π
6
个单位，得到函数y=2sin（x+
π
3
）图象．
其中真命题的个数是（　　）
A、4B、1C、2D、3
在西部大开发中，某市的投资环境不断改善，综合竞争力不断提高，今年一季度先后有甲、乙、丙三个国际投资考察团来到该市，独立地对A，B，C，D四个项目的投资环境进行考察．若甲考察团对项目A满意且对项目B，C，D三个中至少有1个项目满意，则决定到该市投资；否则，就放弃到该市投资．假设甲考察团对A，B，C，D四个项目的考察互不影响，且对这四个项目考察满意的概率分别如下：
（1）求甲考察团决定到该市投资的概率；
（2）假设乙、丙考察团决定到该市投资的概率都与甲相等，记甲、乙、丙三个考察团中决定到该市投资的考察团个数为随机变量ξ，求ξ的分布列和期望．
考察项目ABCD
满意的概率
5
7
2
3
1
2
3
5
关于下列命题：
①若函数y=2x的定义域是{x|x≤0}，则它的值域是{y|y≤1}；
②若函数y=
1
x
的定义域是{x|x＞2}，则它的值域是{y|y≤
1
2
}；
③若函数y=x2的定义域是{x|-2≤x≤2}，则它的值域是{y|0≤y≤4}；
④若函数y=log2x的定义域是{y|y≤3}，则它的值域是{x|0＜x≤8}；
其中不正确的命题序号是
 
．（注：把你认为不正确的命题的序号都填上．）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网