题目内容

12．已知a，b为异面直线．对空间中任意一点P，存在过点P的直线（　　）
A．与a，b都相交B．与a，b都垂直C．与a平行，与b垂直D．与a，b都平行

分析 对4个选项分别进行判断，即可得出结论．

解答 解：过直线a存在一个与直线b平行的平面，当点P在这个平面内且不在直线a上时，就不满足结论，故A错误；
a，b为异面直线，过空间任意一点P，一定能作一条且只能作一条直线l与a，b都垂直，故B正确．
a，b垂直时，C才正确；
若D成立，则a，b平行，D不正确．
故选：B．

点评 本题主要考查了空间中直线与平面之间的位置关系，以及反证法的应用，同时考查了推理能力，属于基础题．

练习册系列答案
相关题目
20．已知函数f（x）=-x3+x2，g（x）=alnx，a∈R．若对任意x∈[1，e]，都有g（x）≥-x2+（a+2）x恒成立，求a的取值范围．
3．已知矩阵M=$[\begin{array}{l}{1}&{b}\\{c}&{2}\end{array}]$有特征值λ1=4及对应的一个特征向量$\overrightarrow{{e}_{1}}$=$[\begin{array}{l}{2}\\{3}\end{array}]$．求矩阵M及另一个特征值λ2和特征向量$\overrightarrow{{e}_{2}}$．
20．已知抛物线C：y2=2px（p＞0）的焦点为F（1，0），抛物线E：x2=2py的焦点为M．
（1）若过点M的直线l与抛物线C有且只有一个交点，求直线l的方程；
（2）若直线MF与抛物线C交于A、B两点，求△OAB的面积．
7．若复数z满足iz=3+5i，则在复平面内复数$\overline{z}$对应的点的坐标是（　　）
A．（3，5）B．（3，-5）C．（5，-3）D．（5，3）
17．在△ABC中，内角A，B，C所对的边分别是a，b，c．已知acosB=bcosA，边BC上的中线长为4．
（Ⅰ）若$A=\frac{π}{6}$，求c；
（Ⅱ）求△ABC面积的最大值．
4．已知$f（x）=\left\{\begin{array}{l}{x^2}-5x-6，x＜4\\ 2-{log_2}x，x≥4\end{array}\right.$
（1）求f（x）的零点；
（2）求f（x）的值域．
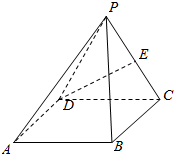1．如图，四棱锥P-ABCD中，底面四边形ABCD是正方形，侧面PDC是边长为a的正三角形，且平面PDC⊥底面ABCD，E为PC的中点．
（1）求异面直线PA与DE所成的角的余弦值；
（2）求点D到面PAB的距离．
2．以椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$的左焦点F1为圆心，过此椭圆右顶点A的圆截直线3x+4y-21=0所得的弦长为$4\sqrt{7}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网