题目内容
7.若复数z满足iz=3+5i,则在复平面内复数$\overline{z}$对应的点的坐标是( )| A. | (3,5) | B. | (3,-5) | C. | (5,-3) | D. | (5,3) |
分析 由iz=3+5i,利用复数代数形式的乘除运算化简得到z,然后求出$\overline{z}$,则在复平面内复数$\overline{z}$对应的点的坐标可求.
解答 解:由iz=3+5i,
得z=$\frac{3+5i}{i}=\frac{-i•(3+5i)}{i•(-i)}=5+3i$,
∴$\overline{z}=5-3i$.
则在复平面内复数$\overline{z}$对应的点的坐标是:(5,-3).
故选:C.
点评 本题考查了复数的代数表示法及其几何意义,考查了共轭复数的求法,是基础题.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
12.已知a,b为异面直线.对空间中任意一点P,存在过点P的直线( )
| A. | 与a,b都相交 | B. | 与a,b都垂直 | C. | 与a平行,与b垂直 | D. | 与a,b都平行 |
19.已知a,b为实数,则( )
| A. | (a+b)2≤4ab,$a+b≤\sqrt{2{a^2}+2{b^2}}$ | B. | (a+b)2≥4ab,$a+b≤\sqrt{2{a^2}+2{b^2}}$ | ||
| C. | (a+b)2≤4ab,$a+b≥\sqrt{2{a^2}+2{b^2}}$ | D. | (a+b)2≥4ab,$a+b≥\sqrt{2{a^2}+2{b^2}}$ |
17.某三棱锥的三视图如图所示,则该三棱锥四个面中,为直角三角形的个数为( )
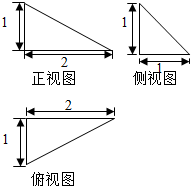

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,D是△ABC外接圆上的一点,弦AD与BC交于点E,且AB=AC=6,AE=4.
如图,D是△ABC外接圆上的一点,弦AD与BC交于点E,且AB=AC=6,AE=4.